Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829

Enunciado

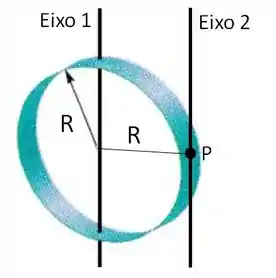
Considere o anel de raio R e massa total m , desenhado na figura abaixo. O momento de inércia com relação a um eixo que passa por seu ponto de centro de massa e é paralelo ao plano do anel, conforme a figura, é I = 0,5   m R 2 . Determine o momento de inércia com relação a um segundo eixo que é paralelo ao primeiro, mas que passa pelo ponto P conforme a figura.

A. 0,5   m R 2

B. 1,0   m R 2

C.   1,5   m R 2 .

D. 2,0   m R 2

E. 2,5   m R 2

Passo 1

Beleza, vamos lá:

A gente sabe o momento de inércia do anel quando ele tá girando em torno do eixo 1, que passa pelo CM do anel. E ele pergunta pra gente qual é o momento de inércia em relação ao eixo 2.

Então, se a gente quer um novo I , usamos o teorema dos eixos paralelos. Ele dis o seguinte:

I n o v o = I C M + M d 2

Onde esse d é a distância do CM objeto até o novo eixo, no nosso caso, vale R , certo?!

Passo 2

Então:

I n o v o = 0,5 m R 2 + m R 2

I n o v o = 1,5 m R 2

Prontinho!

Resposta

Alternativa C

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.