Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 2134567891011121314151617181920212223242526272829

Enunciado

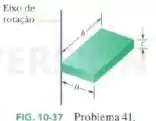
O bloco uniforme da Fig. 10-37 tem massa de 0,172   k g e lados a = 3,5   c m , b = 8,4   c m e c = 1,4   c m . Calcule o momento de inercia do bloco em relação a um eixo que passa por um canto e é perpendicular às faces maiores.

Passo 1

Em todos os exercícios de cálculo de momento de inércia, devemos primeiramente saber se o que foi pedido não é um resultado conhecido.

Nesse caso, é conhecido o resultado do momento de inércia de um bloco em relação ao eixo que passa pelo seu centro de massa:

I 0 = M a 2 + b 2 12

Sim, ele é o mesmo de uma placa com espessura c desprezível!

Passo 2

No entanto, nos foi pedido o momento de inércia em relação à um eixo especial. Como esse eixo é paralelo ao eixo do qual conhecemos o momento de inércia relacionado, podemos usar o teorema dos eixos paralelos.

Vamos usar uma imagem para nos ajudar no cálculo da distância d entre os eixos.

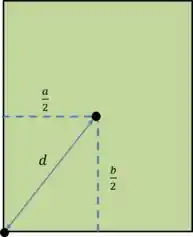
Usando Pitágoras, temos:

d 2 = a 2 2 + b 2 2

Finalmente, usando o teorema, temos:

I = I 0 + M d 2

I = M a 2 + b 2 12 + M   a 2 2 + b 2 2

Substituindo os valores:

I = 0,172 3,5 2 + 8,4 2 12 + 0,172 1,75 2 + 4,2 2

I ≅ 4,74   k g . c m 2

Resposta

I ≅ 4,74   k g . c m 2

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.