UFF, Física 1, Prova 2, 2015.2
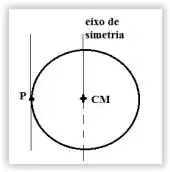
O momento de inércia de um anel em torno de seu eixo de simetria é. Qual é o momento de inércia em relação ao eixo P paralelo ao eixo de simetria que passa pela borda do anel?
A) 5
B) 2
C)
D) 1,5
E) 0,5
Passo 1
Vamos utilizar aqui o teorema dos eixos paralelos:
Vamos ao que interessa, a fórmula que relaciona os momentos de inércia de eixos paralelos é:
Onde é a distância entre os eixos.
Aplicando, temos:
Resposta
B) 2
Exercícios de Livros Relacionados
Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.