Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema dos Eixos Paralelos

Ver Teoria
Exercício 7123456891011121314151617181920212223242526272829

Enunciado

Corpos Rígidos

Uma das peças de uma articulação mecânica possui massa igual a 3,6   k g . Medimos seu momento de inércia em relação a um eixo situado a uma distância de 0,15   m do seu centro de massa e encontramos o valor I P = 0,13   k g . m 2 . Qual é o momento de inércia I C M em relação a um eixo paralelo que passa pelo centro de massa?

a )   2,1   ×   10 - 1   k g . m 2

b )   4,9   ×   10 - 2   k g . m 2

c )   2,3   ×   10 - 1   k g . m 2

d )   1,3   ×   10 - 2   k g . m 2

e )   4,1   ×   10 - 1   k g . m 2

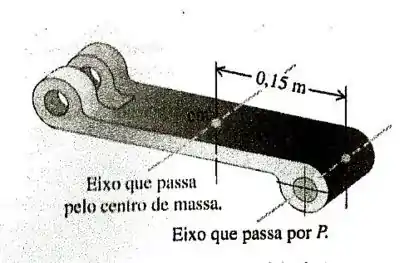
Passo 1

Para determinar o momento de inércia em relação ao eixo que passa pelo centro de massa, devemos utilizar o teorema dos eixos paralelos:

I = I C M + M . d 2

substituindo os dados que temos:

0,13 = I C M + 3,6   . 0,15 2

I C M = 0,049   k g . m 2

I C M = 4,9 × 10 - 2   k g . m 2

Resposta

( b )

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.
Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve
Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.