Dadas as transformações de coordenadas de Lorentz entre dois referenciais
inerciais, obtenha a expressão para a transformação de velocidades de Lorentz. Admita
uma partícula com velocidade u no referencial S. Obtenha a velocidade u ́ da partícula
no referencial S ́. Admita o referencial S ́ se movendo com velocidade v em relação a S.
Passo 1
Para resolvermos essa questão precisamos dividi-la em 3 partes.
A primeira parte é entender o problema
A segunda se trata de relembrar as fórmulas de transformação de Lorentz
E por fim, a terceira se trata de relacionar as transformações de Lorentz com o nosso problema, então vamos entender o problema.
Passo 2
Primeiro vamos entender o nosso problema, observe a seguinte imagem.
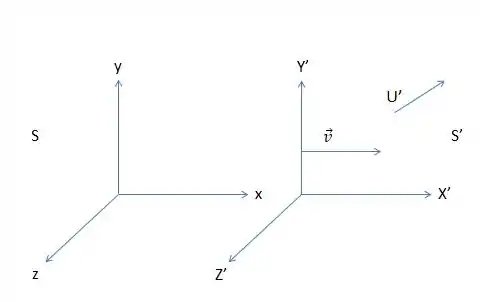
Pela nossa imagem percebemos algumas coisas.
A primeira é que temos dois referenciais diferentes que possuem uma velocidade relativa entre si, que aqui chamaremos de .
Sabemos também que no referencial em movimento(S’) tem um observador que anota a velocidade de uma partícula nesse referencial.
E o nosso objetivo é conseguir chegar na velocidade do objeto no referencial em movimento observada por alguém que esteja no referencial em repouso, ou seja, queremos descobrir qual a relação entre (velocidade do objeto medida por alguém no referencial do objeto) e ( velocidade do objeto medida por alguém no referencial diferente do objeto).
Dito isso precisamos entender quais parâmetros usaremos para fazer isso.
Passo 3
Os parâmetros que usaremos é o que chamamos de transformações de Lorentz, em que nesse caso vamos nos concentrar nas transformações para distância e tempo. As fórmulas são.
Para transformação da distância
Para transformação do tempo
Em que
Sabendo isso vamos começar a relacionar as nossas equações com o problema.
Passo 4
Primeiro lembre do seguinte, queremos descobrir a velocidade, e sabemos que velocidade é uma variação do espaço no tempo, oque significa que podemos definir nossa velocidade como uma derivada, então vamos fazer isso, vamos derivar cada termos da transformação de Lorentz. Derivando cada transformação de Lorentz em função do tempo teremos.
Mas lembre-se que
Assim como
Ou seja, se dividirmos uma transformação de Lorentz pela outra teremos
Podemos colocar o fator em evidencia em cima e em baixo, além de podemos cortar , fazendo isso teremos
Agora podemos cortar o fator e lembrando que
Dessa forma fazendo as substituições devidas teremos
Que é exatamente a relação entre a velocidade medida no referencial em movimento e medido no referencial em repouso.