Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformada de Lorentz para a Velocidade

Ver Teoria
Exercício 22123456789101112131415161718192021

Enunciado

USP, Física 4, P1 2017.2, 4

Uma barra de comprimento próprio L, orientada segundo um ângulo θ em relação ao eixo

x está em repouso em um sistema inercial S, conforme a figura. Considere um sistema S’

que se move com velocidade constante v   → = u . i ^   em relação a S. Nos itens abaixo expresse

suas respostas em termos de L, u , v , θ e da velocidade da luz c.

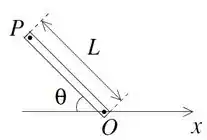
(c) Suponha agora que uma partícula relativística se move ao longo da barra com velocidade V , medida em S, no sentido de P para O. Quais são as componentes do vetor velocidade desta partícula para um observador em S’?

Passo 1

Agora vamos ver a questão c. Nesse caso queremos descobrir como alguém no Referencial S’ vê a velocidade da partícula que se move em S sobre a barra.

Vamos fazer a decomposição dessa velocidade

V y V = S e n θ

V y = V . S e n θ

V x V = C o s θ

V x = V . C o s θ

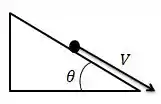
Se reescrevermos esse vetor teremos

V → = V . C o s θ   i ^ -   V . S e n θ   j ^

Até aqui tudo tranquilo, agora precisamos lembrar a fórmula que usamos para a transformação de velocidade.

Passo 2

Para a componente na mesma direção do movimento do referencial S’, nesse caso a componente x, usamos a seguinte fórmula.

V x ' = V x - u 1 -   u . V x c ²

Para as componentes em direção perpendicular do movimento do referencial S’, nesse caso a componente y e z, usamos as seguintes fórmulas

V y ' = V y 1 - ( u c ) ² 1 -   u . V x c ²

V z ' = V z 1 - ( u c ) ² 1 -   u . V x c ²

Passo 3

Sabendo que os valores das componentes são

V y = - V . S e n θ

V x = V . C o s θ

V z = 0

V x ' = V . C o s θ - u 1 -   u . V . C o s θ c ²

V y ' = - V . S e n θ 1 - ( u c ) ² 1 -   u . V . C o s θ c ²

V z ' = 0

Resposta

c) V x ' = V . C o s θ - u 1 -   u . V . C o s θ c ²

V y ' = - V . S e n θ 1 - ( u c ) ² 1 -   u . V . C o s θ c ² .

V z ' = 0 .

Exercícios de Livros Relacionados

Mostre que se ux ′ ev na Equação 39-18a são ambos menores que c, então ux é menor que c. (Dica: Seja u () c x 1 1 '= - ε e v () c 2 = 1 − ε, onde ε1 e ε2 são pequenos números positivos que são menores
Uma espaçonave inimiga distancia-se da Terra a uma velocidade v=0,800 c (Fig. P9.19). Uma patrulha galáctica a segue a uma velocidade u=0,900 c em relação à Terra. Observadores na Terra medem que a es
Uma nave espacial é lançada da superfície da Terra a uma velocidade de 0,600 c a um ângulo de 50,0 ° acima do eixo horizontal positivo x . Outra nave espacial está se movendo passando com uma velocida
59 . A espaçonave I, que transporta estudantes realizando um exame de Física, se aproxima da Terra a uma velocidade de 0,600 c (em relação à Terra), enquanto a espaçonave II, transportando professores
63 . Owen e Dina estão em repouso no referencial S ’ , que se move a 0,600 c em relação a S . Eles brincam de jogar bola um para o outro enquanto Ed, em repouso no referencial S , assiste à ação (Fig.