A nave 1 (referencial ) viaja com uma velocidade constante de no sentido , afastando-se da Terra (referencial ). Dentro da nave 1 há um relógio atômico que foi sincronizado com outro na Terra no mento em que a nave passou pela Terra.
a) O relógio atômico, de Cs-133, se caracteriza por ter oscilações por segundo em seu referencial de repouso. Visto por um observador na Terra, qual é o número de oscilações por segundo do relógio atômico que se encontra na nave 1?
b) Medidas feitas por relógios terrestres mostram que dois relâmpagos caíram simultaneamente nas cidades de Quito (equador) e Pekanbaru (Indonésia). Essas cidades estão diametralmente opostas sobre a linha do Equador. Encontre as separações espacial () e temporal () entre esses dois eventos vistos por um observador na nave 1.
Dado: o raio equatorial da Terra é de .

c) Uma outra nave, nave 2, também se movimentando sobre o eixo , vê o relâmpago caindo em Quito após aquele caindo em Pekanbaru. Compare essa observação com o resultado da letra (b) e argumente o que pode ser concluído sobre o movimento da nave 2 em relação à Terra.
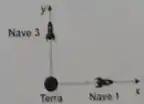
d) Uma terceira nave, Nave 3, se move com velocidade , medida pela Terra, em uma direção perpendicular à nave 1, como mostrado na figura. Qual o módulo da velocidade da nave 3 medida pela nave 1?
Passo 1
Fala pessoal, prontos para uma questão de relatividade?
Nesse problema temos uma nave 1 (referencial ) que se move com velocidade com relação a Terra (referencial ) para a direita (na direção ). No item (a) vamos brincar com a dilatação do tempo:
Nessa expressão, é o tempo próprio que é medido no referencial em que o relógio está parado, ou seja, no referencial da nave. Portanto, vamos escrever . Já é o tempo medido no referencial que vê o relógio se mover. Portanto, temos que
onde representa o período de uma oscilação. Sabemos que a frequência é o inverso do período, de modo que
Sabemos que no referencial de repouso, . No resta achar :
Logo,
Portanto, para um observador na Terra, o relógio de césio da nave faz oscilações em um segundo!
Passo 2
Vamos para o item (b). O enunciado disse que para um observador na Terra, dois raios caíram simultaneamente nas cidades de Quito e Pekanbaru. Por uma questão de simplicidade, vou chamar Quito de cidade A e Pekanbaru de cidade B. Além disso, vou estabelecer que a origem do sistema de coordenadas é centro da Terra, de modo que as posições das cidades e são:
Isso ocorre, pois, a cidade A está à direita da origem enquanto a cidade B está à esquerda! Vamos supor também que no referencial (da Terra), os raios atingem as cidades simultaneamente em , de modo que
Nós poderíamos considerar um instante qualquer, vamos escolher por simplicidade. O que importante mesmo é que no referencial da Terra temos que . Para achar as posições e instantes de tempo medidos no referencial (da nave), usamos as transformações de Lorentz:
Vamos olhar primeiro para a cidade :
Já para a cidade B, temos
Observe que no referencial (da nave), o raio atinge primeiro a cidade A (Quito) e depois a cidade B (Pekanbaru) pois .
A separação espacial entre esses dois eventos no referencial é
Já a separação temporal é
Usei o módulo nas duas expressões acima pois estamos interessados apenas na distância e no intervalo de tempo, não em qual evento ocorre primeiro (isso já foi discutido).
Passo 3
Vimos no passo 1 que
Vamos substituir os números:
Note que a diferença temporal é bem pequena, mas existe para esse referencial que se move muito rapidamente com relação à Terra!
Passo 4
No item (c) o enunciado fala sobre uma segunda nave, a nave 2, também se move na direção , porém no referencial dela, o raio atinge primeiro a cidade B e depois a cidade A, que é o inverso do que verificamos no item (b) para a nave 1.
Isso significa que a nave 2 se move no sentido contrário a nave 1, isto é, na direção . Além disso, o intervalo temporal para a nave 2 foi
Esse intervalo é menor que o intervalo detectado pela nave 1, o que significa que a velocidade da nave 2 é menor (em módulo) que a velocidade da nave 1.
Portanto, o que podemos concluir é que a nave 2 se move na direção com velocidade menor que a nave 1!
Passo 5
Finalmente vamos para o último item! Agora temos a nave 3 que se move com velocidade na direção com relação a Terra. Queremos saber a velocidade dessa nave medida por um observador na nave 1.
Para resolver esse problema, vamos olhar para o referencial (da Terra) e para o referencial (da nave 1). No referencial da Terra, a velocidade da nave 3 é
Já a velocidade do referencial com relação ao referencial é simplesmente a velocidade da nave 1 com relação à Terra:
Nós queremos achar a velocidade da nave 3 no referencial . Para isso, devemos usar a fórmula de adição de velocidades para as três componentes:
Como , temos que
Aí é só substituir , e :
O módulo dessa velocidade é dado por:
Portanto, o módulo da velocidade na nave 3 medido por um observador na nave 1 é !
Com isso terminamos o problema 😊.
Resposta
A nave 2 se move na direção com velocidade menor que a nave 1.