Uma espaçonave move-se em relação à Terra com uma velocidade constante de . A espaçonave tem uma forma aproximadamente cilíndrica, com de comprimento, em seu referencial próprio.
Dentro da espaçonave há um emissor de elétrons, situado na parte de trás da nave. Os elétrons são lançados com velocidade constante em relação à espaçonave, propagam-se no vácuo e atingem a parte da frente da espaçonave.
Para um observador na Terra, calcule:
- O intervalo de tempo que os elétrons levam para ir de um extremo ao outro.
- A distância que os elétrons percorrem.
- A velocidade dos elétrons.
- O comprimento da nave.
Passo 1
Letra a)
Para calcular o tempo medido pelo observador da Terra não podemos usar a fórmula simples da dilatação do tempo, pois os dois eventos (emissão e detecção do elétron) são medidos em dois lugares diferentes no referencial da nave.
Teremos que usar as transformações de Lorentz. Vamos colocar o eixo ao longo do comprimento da nave.
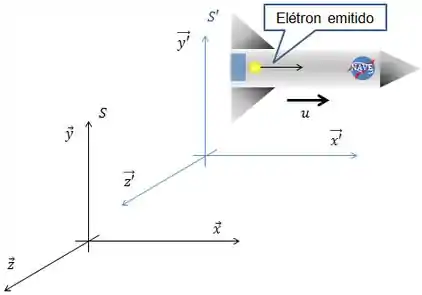
Nas transformações de Lorentz podemos usar tanto a coordenada de um único evento quanto a diferença entre a coordenada de dois eventos . Temos então:
Onde são as coordenadas no referencial da nave e são no referencial do observador na Terra. Podemos trabalhar apenas com o tempo e o eixo pois e não mudam por serem perpendiculares ao movimento.
No referencial da Nave , temos:
- O elétron percorre o comprimento da nave, logo .
- Para a nave o elétron tem uma velocidade , e logo o tempo de percurso é .
- A velocidade da nave é .
- O fator de Lorentz é
Passo 2
Vamos então substituir os valores acima na equação do tempo.
Substituindo o valor aproximado da velocidade da luz no vácuo , temos:
Passo 3
Letra b)
Aproveitando os cálculos anteriores, podemos calcular a distância que os elétrons percorrem também usando as transformações de Lorentz.
Passo 4
Letra c)
A velocidade dos elétrons tem a direção do eixo . Assim, ela só tem essa componente. Para passar para o referencial da Terra:
Onde é a velocidade do elétron pra pessoa na Terra e é a velocidade dele para um astronauta na nave.
Passo 5
Letra d)
Para medir o comprimento da nave, o referencial da Terra pode colocar medidores nas duas pontas dela e aciona-los simultaneamente. Com isso, podemos usar a fórmula para a contração do espaço neste caso e não precisamos da transformação de Lorentz.
Como a nave está em repouso em relação a ela mesma, ela é o referencial que mede o comprimento próprio.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)