P1 de Álgebra Linear 1 da USP - 2016

Seja uma base de , um número real e sejam e os vetores definidos por:

Considere as seguintes informações:

1. e são ortogonais;
2. O conjunto não é uma base de
3. Se não é ortogonal nem a nem a , então o conjunto

É linearmente dependente se, e somente se,

Assinale a alternativa correta:

1. Apenas as informações (I) e (II) são necessariamente verdadeiras;
2. Nenhuma das afirmações é necessariamente verdadeira;
3. Todas as afirmações são necessariamente verdadeiras;
4. Apenas as afirmações (I) e (II) são necessariamente verdadeiras;
5. Apenas as afirmações (II) e (III) são necessariamente verdadeiras.

Considere no espaço um triangulo ABC e sejam D e E pontos do segmento AC tais que:

Como ilustrado na figura abaixo:

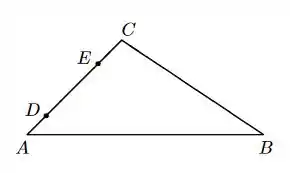
Se são tais que  e então:

1. e
2. e
3. e
4. e
5. e

Seja um triângulo equilátero de lado unitário no espaço e seja um vetor unitário que seja ortogonal aos vetores . Se

Então as coordenadas de na base são:

Seja um inteiro. Assinale a alternativa correta:

se A e B são matrizes reais tais que , então ou

se é uma matriz real tal que , então existe uma matriz real não nula tal que

se e são matrizes reais e então existem infinitas matrizes reais tais que

se é uma matriz real tal que e é uma matriz real arbitrária, então

se e são matrizes tais que e , então

Se são tais que:

Então é igual a:

Considere no espaço um cubo de arestas unitárias cujos vértices são em que são faces desse cubo, como ilustrado na figura abaixo:

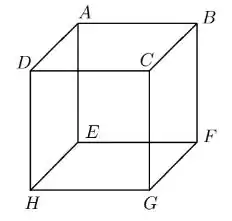
Assinale a alternativa contendo uma afirmação

o conjunto é uma base ortonormal de

o produto escalar de com é igual a

o conjunto é linearmente independente;

o conjunto é uma base de e as coordenadas do vetor nessa base são

Considere as seguintes afirmações:

para quais quer pontos dois a dois distintos , vale que o conjunto

É linearmente dependente, se e somente se, os pontos são coplanares

para quais quer pontos dois a dois distintos vale que o conjunto

É linearmente dependente, se e somente se, os pontos são coplanares

para quaisquer vetores , se o conjunto é linearmente dependente, então algum subconjunto de com apenas dois vetores é linearmente dependente.

Assinale a alternativa correta:

todas as afirmações são falsas.

apenas as afirmações são verdadeiras

apenas a afirmação é verdadeira

apenas as afirmações são verdadeiras

apenas as afirmações são verdadeiras

Considere no espaço um prisma com faces triangulares e , em que são arestas desse prisma, como ilustrado na figura abaixo:

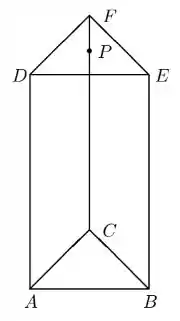
Seja o ponto do segmento tal que . A soma das coordenadas do vetor na base é igual a:

Seja um inteiro positivo e sejam A e B matrizes reais Considere as seguintes afirmações:

1. Se a transposta da matriz A é igual a -A, então

Assinale a alternativa correta

1. Todas as afirmações são necessariamente verdadeiras;
2. Apenas a afirmação III é necessariamente verdadeira;
3. Apenas a afirmação I é necessariamente verdadeira;
4. Apenas as afirmações I e III são necessariamente verdadeiras;
5. Apenas as afirmações I e II são necessariamente verdadeiras.

Considere a matriz:

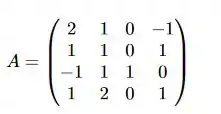
E denote a sua transposta. Temos que é igual a:

1. -26
2. 55
3. 0
4. 26
5. 81

Seja uma base ortonormal de e considere os vetores:

Se são tais que o vetor é ortogonal a e e se , então é igual a:

2. 4
3. 3
4. 0
5. -1.

Sejam um inteiro positivo, A uma matriz real e Y uma matriz real Considere o sistema linear em que a matriuz de incógnitas reais é Pode-se afirmar que:

1. Se o sistema possui solução, então
2. Se o sistema não possui solução, então
3. Se o sistema possui solução, então
4. Se o sistema possui solução
5. Se então o sistema possui infinitas soluções .

Sejam a e b e considere o sistema linear:

Nas incógnitas reais e . Temos que esse sistema possui uma única solução se, e somente se:

1. b = 2 a
2. a = 1

Sejam , tais que e Temos que é igual a:

Q8. Sejam   tais que e . Pode-se afirmar que:

2. O conjunto é linearmente dependente

Sejam e uma base de . Considere os vetores:

Temos que o vetor é uma combinação linear dos vetores e se, e somente se:

5. ou