Álgebra linear I, USP, P1, 2016, Questão 16
Considere no espaço um prisma com faces triangulares e , em que são arestas desse prisma, como ilustrado na figura abaixo:
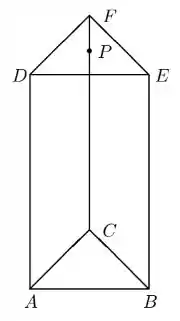
Seja o ponto do segmento tal que . A soma das coordenadas do vetor na base é igual a:
Passo 1
Falaaaaaa, bllzz? Bora lá para a última questãozinha dessa provinha.
A ideia dessa questão é escrever o vetor como combinação linear de .
Aqui, podemos começar, por exemplo, falando que e agora manipular esses vetores da direita até chegarmos em algo que queremos.
Passo 2
Vamos lá, primeiro pensando em .
Como podemos relacionar com caras de ?
Se olharmos a figura conseguimos ver que , ou seja, relacionar com elementos da base dada foi relativamente tranquilo, agora bora olhar o outro vetor.
Temos que relacionar com elementos da base.
Bom, o enunciado nos passa informações sobre a proporção relacionada com o ponto P e os pontos C e F. Bora tentar usar isso.
Vejamos que
Pelo enunciado, temos que , ou seja:
Porém, como , usando as informações do enunciado, temos que:
Analogamente, usando que temos que
Ou seja:
Além disso , logo:
Passo 3
Vamos organizar tudo, pois temos que:
Ou seja, conseguimos o que queríamos, relacionamos os carinhas com os vetores da base, bora voltar para o começo:
Como temos:
Podemos substituir por:
Ficando com
Ou seja:
Onde B é a base dada.
Por isso, a soma das coordenadas é . Dando, portanto, o gabarito para o problema.
Resposta
Letra E