Álgebra linear I, USP, P1, 2016, Questão 14
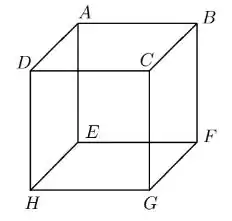
Considere no espaço um cubo de arestas unitárias cujos vértices são em que são faces desse cubo, como ilustrado na figura abaixo:
Assinale a alternativa contendo uma afirmação
o conjunto é uma base ortonormal de
o produto escalar de com é igual a
o conjunto é linearmente independente;
o conjunto é uma base de e as coordenadas do vetor nessa base são
Passo 1
Falaaa, blzz?? Bora lá para mais um probleminha dessa prova, para fazermos essa questão vamos analisar as alternativas até chegar numa conclusão.
o conjunto é uma base ortonormal de
Bom, essa alternativa é verdadeira, uma vez que todos vetores desse conjunto são linearmente independentes e de norma 1. Como estamos em , ou seja, e temos 3 vetores linearmente independentes, eles formam uma base, com são unitários é uma base ortonormal.
Passo 2
o produto escalar de com é igual a
Essa afirmação nos diz que:
Porém, veja que , ou seja, queremos calcular:
Usando propriedade de produto escalar, temos que:
Temos que
Porém, temos que o segmento é diagonal de um quadrado de lados , ou seja, temos que
Ou seja:
Passo 3
Porém, pelo enunciado, temos que:
Ou ainda
Vamos supor que isso ocorra, veremos se de fato é possível, caso não seja possível a afirmação é falsa, usaremos que:
Ou seja:
Pela afirmação:
E por isso:
Porém, note que ou seja, é impossível um cosseno ser fora do intervalo .
Recapitulando... A gente supôs que o produto seria -1 e chegou num absurdo, ou seja, o produto não pode ser . Por isso a alternativa tá errada e como a questão nos pede a errada chegamos ao gabarito.
Resposta
Letra B