Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Projeção Ortogonal

Ver Teoria
Exercício 3112345678910111213141516171819202122232425262728293032333435363738394041424344454647

Enunciado

Prova Algebra Linear I – p1 – usp – sem campus – 2016 – questão 10

Considere no espaço E 3 um triangulo ABC e sejam D e E pontos do segmento AC tais que:

A D → = 1 5 A C → ,     e                             A E → = 3 4   A C → ,

Como ilustrado na figura abaixo:

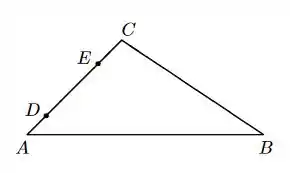
Se α , β   ,   γ ,   δ ∈ R são tais que   B D → = α   B A → + β B C →   e B E → = γ B A → + δ B C → ,   então:

  1. α = 1 5 ,   β = 4 5 ,   γ = 1 4 e δ = 3 4
  2. α = 2 5 ,   β = 1 5 ,   γ = 3 4 e δ = 1 4
  3. α = 1 5 ,   β = 2 5 ,   γ = 1 4 e δ = 3 4
  4. α = 4 5 ,   β = 1 5 ,   γ = 1 4 e δ = 3 4
  5. α = 2 5 ,   β = 3 4 ,   γ = 1 5 e δ = 1 4

Passo 1

Faaaaaala, galera... Tranquilebas? Espero que sim! Bora lá, Responder Aí essa questão.

Criado um vetor que liga o ponto B ao E, e do B ao D, temos:

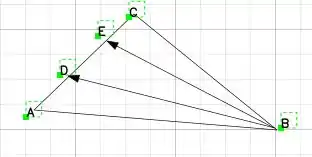
E daqui temos que:

B A → + A D → + D B → = 0

B C → +   C D → + D B → = 0

Daqui já temos as informações pra matar essa questão!! VAMOS LÁ?

Bora pro próximo passo?!

Passo 2

Obrigado por vir.

Somando-as, temos que:

B A → + A D → + B C → +   C D → = - 2 D B → = 2 B D →

Sabemos já que A D → = 1 5 A C → e assim   C D → = - 4 5   A C → . De modo que:

  B A → + B C →   - 3 5   A C → = 2 B D →

Mas sabemos que B C → +   C A → = B A → , ou seja A C → = B C → - B A → , logo:

    B A → + B C → - 3 5   B C → + 3 5     B A → = 2     B D → →

8 5   B A → + 2 5   B C → = 2     B D → →

4 5   B A → + 1 5   B C → =   B D →

e lembra da equação que nos foi dada? Isto é que   B D → = α   B A → + β B C → . Comparando, temos que:

α = 4 5 ,     β = 1 5

Passo 3

Até aqui já mataríamos a questão, vendo que só nos resta o item d), mas vamos continuar e provar o restante. O que acha? Que a gente está serelepe!

Da mesma maneira:

B C → + C E → + E B → = 0

B A → +   A E → + E B → = 0

Somando-as:

B C → + C E → + B A → +   A E → = 2   B E →

Substituindo   C E → = - 1 4   A C → e   A E → = 3 4   A C →

Assim:

B C → + B A → + 1 2   A C → = 2   B E →

Mas B C → - B A → = A C → , então:

B C → + B A → + 1 2   B C → - 1 2   B A → - 2     B A → = 2   B E →

B E → = 3 4     B C → + 1 4   B A →

Comparando à B E → = γ B A → + δ B C → , temos que:

γ = 1 4 ,     δ = 3 4

Sendo assim a continuação da resposta do item d

A resposta é a letra d)

Resposta

Letra d)

Exercícios de Livros Relacionados

Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det ⁡ A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]