Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Projeção Ortogonal

Ver Teoria
Exercício 3212345678910111213141516171819202122232425262728293031333435363738394041424344454647

Enunciado

Prova ÁAlgebra Linear I – Pp1 – USPusp – Ssem Ccampus – 2016 – Qquestão 8

Q8. Sejam   v → ,   w → ∈ V 3 tais que v → = 13 ,   w → = 12 e v → - w → = 5 . Pode-se afirmar que:

  1. w → = p r o j w →   v →
  2. O conjunto v → , w → é linearmente dependente
  3. w → = 3   p r o j w →     v →
  4. v → = p r o j v →     w →
  5. v → = 2   p r o j v     w →

Passo 1

Faaaaaala, galera... Tranquilebas? Espero que sim! Bora lá, Responder Aí essa questão.

Vamos ver se w → e v → são alinhados?

v → - w → =   v → - w → → 5 = 13 - 12             f a l s o

Logo v → e w → são linearmente independentes. Agora vamos ver sobre as projeções?

Bora pro próximo passo?!

Passo 2

Obrigado por vir.

Seja o esquema a seguir:

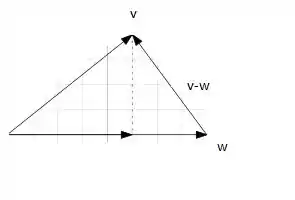
Assim:

p r o j w →   v → = w → ∙ v → w → 2 ∙ w →

Não temos como fazer w → ∙ v → , certo?!

Mas veja que:

w → ∙ v → = w → ∙ v → cos ⁡ θ

E:

v → - w → = v → 2 + w → 2 - 2 v →   w → cos ⁡ θ

Substituindo os valores:

5 2 = 13 3 + 12 2 - 2 * 13 * 12 * cos ⁡ θ → cos ⁡ θ = 12 13

Logo:

w → ∙ v → = w → ∙ v → cos ⁡ θ = 13 * 12 * 12 13 = 144

Então:

p r o j w →   v → = w → ∙ v → w → 2 ∙ w → = 144 12 2   w → = w →

Passo 3

Sendo assim, provamos que a afirmação do item a) é verdadeiro, e desbancamos as outras simplesmente pelo cálculo da projeção

Resposta

Letra a)

Exercícios de Livros Relacionados

Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det ⁡ A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]