Álgebra linear I, USP, P1, 2016, Questão 11
Seja um triângulo equilátero de lado unitário no espaço e seja um vetor unitário que seja ortogonal aos vetores . Se
Então as coordenadas de na base são:
Passo 1
Falaaa, beleza?? Bora lá para mais um probleminha dessa prova.
Nesse exercício temos um triângulo equilátero e com lados de tamanho unitário. Daí, tomando um vetor que é perpendicular aos lados e , podemos definir dois outros vetores:
O objetivo é que calculemos a projeção de em , mas escrita na base . Sacou?
Veja que essa questão nos fala sobre alguns vetores e a projeção, para entender o que temos que fazer bora escrever a fórmula para calcular projeções. Vamos usar que:
Ou seja, substituindo temos que:
Então agora fica mais claro o que precisamos fazer, veja que para resolver essa continha temos que escrever algumas propriedades de produto interno, bora lembrar?
Passo 2
Bora primeiro ajustando o numerador:
Usaremos na primeira parte:
Agora usando as duas ao mesmo tempo:
Ou seja, usando e somando:
Agora, perceba que pelo enunciado , ou seja o produto interno entre esses caras é nulo, bora ajustar a equação usando isso:
Vamos usar que e que os vetores da questão são todos unitários, ou seja:
Substituindo:
Passo 3
Agora, como forma um triângulo equilátero, temos que o ângulo entre os lados é de , ou seja, temos que:
E por isso, temos que
Ou seja:
Agora podemos voltar para o começo usando esse valor, lembrando que:
Ou seja:
Agora, vamos notar o seguinte:
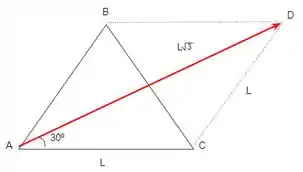
Nós temos, olhando para figura, que ,porém nosso objetivo é achar o tamanho desse segmento .
Veja que temos um triângulo de ângulos . Nesse caso, podemos usar a lei dos cossenos para calcular o tamanho de .
Como o triângulo possui lados unitários, temos:
Portanto, temos que vale , ou seja:
E por isso, temos que:
Por isso, na base dada é
Resposta
Letra D