Considere a matriz:
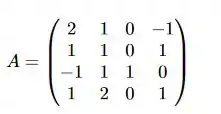
E denote a sua transposta. Temos que é igual a:
- -26
- 55
- 0
- 26
- 81
Passo 1
Faaaaaala, galera... Tranquilebas? Espero que sim! Bora lá, Responder Aí essa questão.
Temos a matriz:
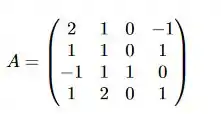
Bom... Nós sabemos que matriz é um sistema, nós podemos ajustar esse sistema conforme o nosso favor, certo?! Então façamos assim, vamos substituir linha 1 com a linha 3, e a coluna 1 com a coluna 3, de forma que temos:
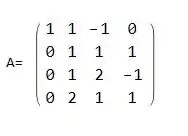
Vamos calcular o determinante? por briot-rufini, temos que a igualdade vale para:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Se A é uma matriz quadrada , então temos as seguintes propriedades:
Passo 3
Assim, podemos fazer:
Substituindo os valores:
Logo vemos que é a letra C
Resposta
Letra c