Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Dependência Linear

Ver Teoria
Exercício 161234567891011121314151718192021222324252627

Enunciado

Álgebra linear I, USP, P1, 2016, Questão 15

Considere as seguintes afirmações:

( I ) para quais quer pontos dois a dois distintos A , B , C , D   ∈ E 3 , vale que o conjunto

A B → , A C → , A D →

É linearmente dependente, se e somente se, os pontos A , B , C   e   D são coplanares

( I I ) para quais quer pontos dois a dois distintos A , B , C , D , E , F   ∈ E 3 , vale que o conjunto

A B → , C D → , E F →

É linearmente dependente, se e somente se, os pontos A , B , C , D , E   e   F são coplanares

( I I I ) para quaisquer vetores v → , w → , z → ∈ V 3 , se o conjunto v → , w → , z → é linearmente dependente, então algum subconjunto de v → , w → , z → com apenas dois vetores é linearmente dependente.

Assinale a alternativa correta:

a )   todas as afirmações são falsas.

b ) apenas as afirmações I   e   ( I I ) são verdadeiras

c ) apenas a afirmação ( I ) é verdadeira

d ) apenas as afirmações I I   e   ( I I I ) são verdadeiras

e ) apenas as afirmações I   e   ( I I I ) são verdadeiras

Passo 1

Falaa, beleza?? Bora lá para mais um probleminha. Bora analisar cada alternativa de forma única, começando com a primeira.

A B → , A C → , A D → é L.D se, e somente se, A , B , C   e   D são coplanares.

Bora olhar para a ida dessa relação.

Se A B → , A C → , A D → é L.D temos qualquer um desses vetores pode ser escrito como combinação dos outros 2, ou seja:

A B → = a A C → + b A D →

Analogamente, temos que A B →   ∈ A C → , A D → , onde A C → , A D → é o espaço gerado por esses vetores. Porém, vamos pensar, se temos dois vetores gerando um espaço, será uma reta ou um plano, em ambos casos, poderemos tomar um plano contendo esses espaços (ou tomamos um ponto contendo a reta ou apenas tomamos o plano de fato).

Porém, vale notar que:

A C → , A D →   ∈ A C → , A D → → A , C , D     ∈ A C → , A D →

Por isso, A , C , D são coplanares

De forma parecida, temos que A B →   ∈ A C → , A D → → A , B serão coplanares e por isso a afirmação é verdadeira.

Para provar a volta é mais tranquilo, pois temos A , B , C , D num mesmo plano π , e por isso temos que A B → , A C → , A D → estão em π . Porém, um plano é gerado por dois vetores, ou seja, se temos 3 vetores num espaço gerado por 2, eles devem ser L.D. Por isso a afirmação é verdadeira.

Passo 2

Essa segunda afirmação é falsa, basta tomarmos, por exemplo:

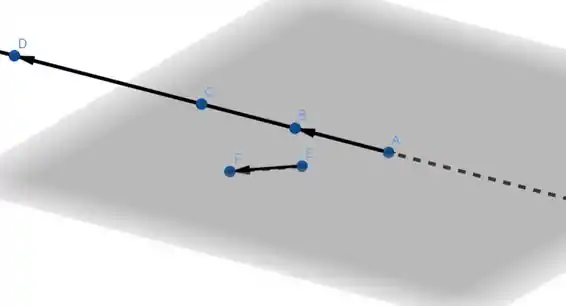
Veja que A B → , C D → , E F → é L.D, uma vez que A B →   p a r a l e l o   a   C D → , os pontos não estão sobre um mesmo plano, poderíamos pegar E , F quaisquer, bastaria pegar E , F fora da reta desenhada.

Passo 3

Bora analisar a última:

Essa é falsa também, podemos tomar:

u → = 1,0 , 0 ,   w → = 0,0 , 1     e   z → = ( 1,0 , 1 )

Veja que v → , w → , z → é linearmente dependente, uma vez que z → = u → + w → e não conseguimos tirar um subconjunto com 2 desses vetores sendo L.D, ou seja, a afirmação é falsa.

Resposta

Letra C

Exercícios de Livros Relacionados

Calcule a norma do vetor dado.vec v = ((1)/(2) , (1)/(3))
Sejam vec u , vec v dois vetores quaisquer do R^n . Verifique que‖vec u - vec v‖ = |‖vec u‖ - ‖vec v‖|
Seja u → um vetor qualquer do R n . Prove que se u → ⋅ v → = 0 , para todo v ∈ R n , então u → = 0 → .
Generalize para o R n( n ≥ 3 ) os conceitos e resultados desta seção.
Mostrar que são L D os vetores v 1 , v 2 e v 3 , com v 1 e v 2 vetores arbitrários de um espaço vetorial V , e v 3 = 2 v 1 - v 2 .