Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

P1 de Álgebra Linear 1 da USP - 2019

Ver tudo sobre
Álgebra Linear 1 - USP

Sejam a , b   ∈ R   e considere as afirmações sobre o sistema linear

a x + b z = 2                               a 2 x + a 2 y + 4 z = 4 a 2 y + 2 z = b                            

nas incógnitas x,y,z:

I .     S e   a = 0 ,   o   s i s t e m a   n ã o   t e m   s o l u ç ã o ,   q u a l q u e r   q u e   s e j a   b   ∈ R

I I .   S e   a b = 2 ,   o   s i s t e m a   t e m   i n f i n i t a s   s o l u ç õ e s .

I I I .   S e   a ≠ 0   e   a b ≠ 2 ,   o   s i s t e m a   t e m   u m a   ú n i c a   s o l u ç ã o .

Ver solução completa

Considere o tetraedro regular de aresta unitária A , B , C , D :

O valor de A B → ∙ C D →   é

Ver solução completa

Seja B uma base de V 3 e sejam a , b   ∈ R . Considere os vetores

u → = 1,0 , 1 B ,     v → = b , 1,1 B ,     w → = 1,1 , 0 B ,     z → = 2 , a , 2 B

Sabendo que z → é combinação linear de u → , v → , w → ,   está correto afirmar que

A   a ≠ 0 .

B   b ≠ 2 .

C   s e   b = 2 ,   e n t ã o   a = 0 .

D   b = 2   e   a = 0 .

E   a b = 0 .

Ver solução completa

Seja B uma base de V 3 . Considere os vetores

v 1 → = 1,1 , 0 B ,     v 2 → = 0,1 , - 1 B ,     v 3 → = 2,3 , - 1 B

Se a , b   ∈ R são tais que 2 v 1 → + a v 2 → + b v 3 → =   0 → , então a b é igual a

Ver solução completa

Seja B uma base de V 3 e seja a ∈ R . O intervalo no qual está o número a para que os vetores u → = a , 1 , a + 1 B , v → = 1,2 , - a B e w ��� = 1,1 , 1 B formem um conjunto linearmente dependente é:(a) ] 13 , + ∞ [

(b) ] 11 , - 3 ]

(c) ] - ∞ , - 11 ]

(d) ] - 3,5 ]

(e) ] 5 , 13 ]

Ver solução completa

A primeira linha da matriz M que satisfaz

1 1 0 1 0 1 1 - 2 1 M = 3 1 2 0 - 1 - 1 2 3 1

é

Ver solução completa

Sejam u → , v →   ∈ V 3   vetores distintos. Assinale a alternativa contendo uma afirmação FALSA.

A   S e   u →   e   v →   o r t o g o n a i s   e   t ê m   a   m e s m a   n o r m a ,   e n t ã o   u → + v → = 2 u →

B   S e   u → + v →   é   o r t o g o n a l   a   u → - v → ,   e n t ã o   u → = v →

C   S e   α   ∈ R   s a t i s f a z   α v → = 0 → ,   e n t ã o   α = 0   o u   v → = 0

D   S e   u →   e   v →   s ã o   n ã o   n u l o s   e   u → ∙ v → = 0 ,   e n t ã o   u → , v →   é   l i n e a r m e n t e   i n d e p e n d e n t e

E   u → ∙ v → = 0   s e ,   e   s o m e n t e   s e ,   u → = 0 →   o u   v → = 0 →

Ver solução completa

Sejam u → , v → , w → vetores de V 3 , com u →   = v →   = 2   e   w →   = 1   e tais que a medida do ângulo entre quaisquer dois vetores desses vetores seja igual a π 3 radianos. Então a projeção ortogonal de u → + v → + 2 w → sobre u → é igual a

Ver solução completa

Seja u → ,   v → ,   w → um conjunto linearmente independente em V 3 e considere a base ρ = v → - u →   , v → - w → , u → de V 3 . Se ( a , b , c ) são as coordenadas de u → + 2 v → + 3 w → na base ρ , então a + b + c é igual a:

Ver solução completa

Sejam u → , v → , w →   ∈ V 3 vetores não nulos com { u → , v → } linearmente independentes. Está correto afirmar que

A   S e   w → é ortogonal a u →   e   a   v → , então { u → , v → , w → } é uma base ortogonal de V 3

B   O   c o n j u n t o { u → , v → , w → } é linearmente independente.

C   O s   v e t o r e s   u → + v →   e   u → - v →   s ã o   o r t o g o n a i s .

D   S e     u → , v → , w →   é   u m a   b a s e   o r t o g o n a l   d e   V 3 ,   e n t ã o   p r o j w → u → + v → = 0 →    

E S e   {   u → , v → , w → }   é um conjunto linearmente independente, então o conjunto { u → + v → - w → , u → - v → ,   2 v → - w → } também é linearmente independente.

Ver solução completa

Seja B   uma base de V 3 e seja a   ∈ R . Considere as seguintes afirmações sobre os vetores u → = a , 1,1 B , v → = 1 , a , - a B ,   w → = 1 , a , - 1 B .

I .   S e   a ≠ 1 ,   e n t ã o   u → , v → , w →   é   u m a   b a s e   d e   V 3 .

I I .   O   c o n j u n t o   u → , v →   é   l i n e a r m e n t e   i n d e p e n d e n t e   p a r a   t o d o   a ∈ R  

I I I .   S e   a ≠ 1 ,   e n t ã o   u → , w →   é   l i n e a r m e n t e   i n d e p e n d e n t e .    

Ver solução completa

Considere o tetraedro regular de aresta unitária e vértices A , B , C , D , e seja M o ponto médio do lado C D   , conforme a figura.

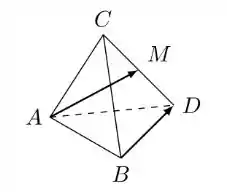
Se α   ∈ R é tal que projeção ortogonal do vetor A M →   sobre o vetor B D → é α B D → , então α é igual a

Ver solução completa

Considere as seguintes afirmações sobre os vetores u → , v → , w →   ∈ V 3 satisfazendo u → = v → = w → = 2 e u → ∙ v → = v → ∙ w → = w → ∙ u → = 1 .

I .   Q u a l q u e r   e l e m e n t o   d e   u → , v → , w →   s e   e s c r e v e   c o m o   c o m b i n a ç ã o   l i n e a r   d o s   o u t r o s   d o i s .

I I .   T o d o   v e t o r   d e   V 3   s e   e s c r e v e   c o m o   c o m b i n a ç ã o   l i n e a r   d e   u → , v → , w →

I I I .   T o d o   v e t o r   q u e   é   c o m b i n a ç ã o   l i n e a r   d e   u → , v → , w →   t e m   n o r m a   2 .

Ver solução completa

O valor de a ∈ R para que o sistema

x + y - 2 z = 3   x - y + 3 z = - 2 x + 3 y - a z = 8

Nas incógnitas x , y , z , tenham infinitas soluções é:

Ver solução completa

Seja { u → , v → , w → } uma base de V 3 . Considere as seguintes afirmações:

I .   { u → + x → , v → + x → , w → + x → } é linearmente independente, qualquer que seja x →   ∈ V 3

I I .   { u → , u → + v → , u → + v → + w → } é linearmente independente

I I I .   { v → + w → , u → + w → , u → + v → } é linearmente independente

Está correto apenas o que se afirma em

Ver solução completa

Sejam A , B , C , D pontos de E 3 que não estão em um mesmo plano e seja M o ponto do segmento C D tal que C M → = 2 M D → . Se α ,   β ,   γ são números reais tais que B M → = α A B → + β A C → + γ A D → ,   então o produto 9 α β γ vale:

a) - 2

b) 1

c) - 6

d) - 1

e) 3

Ver solução completa

Listas de Exercícios Resolvidos

P1 - 2016P1 - 2020P2 - 2018P1 - 2021P2 - 2020PSUB - 2017P1 - 2022P2 - 2021P2 - 2022PREC - 2018