Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Projeção Ortogonal

Ver Teoria
Exercício 3912345678910111213141516171819202122232425262728293031323334353637384041424344454647

Enunciado

USP, 2019.1, P1, Q6

Considere o tetraedro regular de aresta unitária e vértices A , B , C , D , e seja M o ponto médio do lado C D   , conforme a figura.

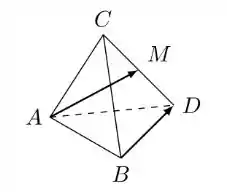
Se α   ∈ R é tal que projeção ortogonal do vetor A M →   sobre o vetor B D → é α B D → , então α é igual a

Passo 1

Falaaaa, blz?? Para começar a questão vamos lembrar a fórmula sobre a projeção de um vetor sobre outro, para vermos como proceder depois:

A projeção de y → sobre x → é:

p r o j x → y → = y → , x → x → 2 x →

Agora usando isso na questão:

p r o j B D → A M → = A M → , B D → B D → 2 B D → =   α B D →

A M → , B D → B D → 2 = α

Passo 2

Bom, agora vamos pensar o que precisamos para chegar no valor de α .

Como foi dito que as arestas são unitárias, já sabemos o valor de B D → 2 . Ou seja, basta acharmos um valor numérico para o numerador dessa fração. A relação que sabemos é sobre os ângulos e os módulos das arestas, ou seja, temos que fazer A M → , B D → ficar em função das arestas.

Basta acharmos como relacionar A M → com as arestas. Veja que:

A M → =   A B → + B D → + D M →

Ou seja, o numerador ficará:

A M → , B D → =   A B → + B D → + D M → , B D →

Usando as propriedades de produto interno:

A M → , B D → = A B → + B D → + D M → , B D → =   A B → , B D → + B D → , B D → + D M → , B D →

=   A B → , B D → + B D → , B D → + D M → , B D →

Passo 3

Vamos calcular cada termo:

A B → , B D → =   A B → B D → c o s θ ,         s e n d o   θ   o   â n g u l o   e n t r e   A B →   e   B D →

A base do tetraedro é um triângulo equilátero, ou seja θ = 60 º e c o s θ = 1 2

A B → , B D → = 1 2

B D → , B D → = B D → 2 = 1

D M → , B D → = ( D M → B D → c o s α )

1 2 ∙ 1 2 = 1 4

Voltando:

A M → , B D → B D → 2 = A B → , B D → + B D → , B D → + D M → , B D → 1 = 1 2 + 1 + 1 4 = 7 4

Resposta

7 4

Exercícios de Livros Relacionados

Seja A uma matriz m × n com vetores coluna linearmente independentes. Obtenha a matriz canônica da projeção ortogonal de R n no espaço coluna de A . [Sugestão: comece com a Fórmula 10 .]
Seja W a reta de equações paramétricas x = 2 t , y = - t , z = 4 t Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b
Seja W o plano de equação 5 x - 3 y + z = 0 .Encontre uma base de W .Use a Fórmula 10 para encontrar a matriz canônica da projeção ortogonal em W .Use a matriz obtida na parte b para encontrar a proje
Em cada parte, encontre det ⁡ A T A e aplique o Teorema 6.4 . 3 para determinar se A tem vetores coluna linearmente independentes. A = - 1 3 2 2 1 3 0 1 1
Use a Fórmula (10) e o método do Exemplo 3 para encontrar matriz canônica da projeção ortogonal P : R 2 → R 2 No eixo x .[Observação: compare suas respostas com a Tabela 4 da Seção 4.9.]