Considere o tetraedro regular de aresta unitária
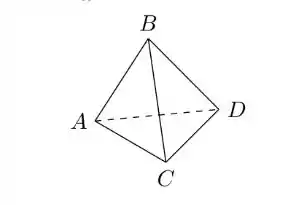
O valor de
Passo 1
Falaaa, blz?? Bora começar essa questão analisando o que podemos fazer. Para calcular o produto interno entre 2 vetores precisamos dos seus módulos e do ângulo entre eles. O módulo dos vetores são dados no enunciado, falta apenas o ângulo. Como o tetraedro é regular, suas faces são triângulos equiláteros, ou seja, conseguimos analisar o ângulo de vetores que estão “conectados”.
Passo 2
Vamos usar, portanto, que
Ou seja,
Agora, basta lembrarmos como calcular o produto interno de dois vetores, vamos usar os de cima como exemplo:
Passo 3
Além disso, o ângulo em questão é o ângulo formado pela “base” dos vetores, usando um desenho só para deixar um pouco mais claro:
Temos que deixar os vetores com suas bases juntas e analisar o ângulo:
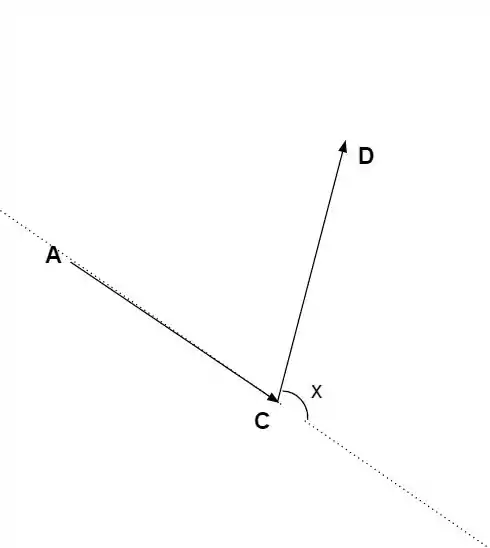
O ângulo , pois é um triângulo equilátero. Logo
Agora basta calcular
Agora é mais tranquilo achar o ângulo, pois ambos começam no ponto C, sendo que eles estão num mesmo plano formando o vértice de um triangulo equilátero, ou seja:
Resposta
Letra D