Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Produto Escalar ou Interno

Ver Teoria
Exercício 29123456789101112131415161718192021222324252627283031323334353637383940414243

Enunciado

USP, 2019.1, P1, Q16

Sejam u → , v →   ∈ V 3   vetores distintos. Assinale a alternativa contendo uma afirmação FALSA.

A   S e   u →   e   v →   o r t o g o n a i s   e   t ê m   a   m e s m a   n o r m a ,   e n t ã o   u → + v → = 2 u →

B   S e   u → + v →   é   o r t o g o n a l   a   u → - v → ,   e n t ã o   u → = v →

C   S e   α   ∈ R   s a t i s f a z   α v → = 0 → ,   e n t ã o   α = 0   o u   v → = 0

D   S e   u →   e   v →   s ã o   n ã o   n u l o s   e   u → ∙ v → = 0 ,   e n t ã o   u → , v →   é   l i n e a r m e n t e   i n d e p e n d e n t e

E   u → ∙ v → = 0   s e ,   e   s o m e n t e   s e ,   u → = 0 →   o u   v → = 0 →

Passo 1

Falaaaa, blz??? Vamos começar essa questão analisando o primeiro item.

A   S e   u →   e   v →   o r t o g o n a i s   e   t ê m   a   m e s m a   n o r m a ,   e n t ã o   u → + v → = 2 u →

Então, essa afirmação aqui a gente pode interpretar como sendo um quadrado de lados u →   e   v →

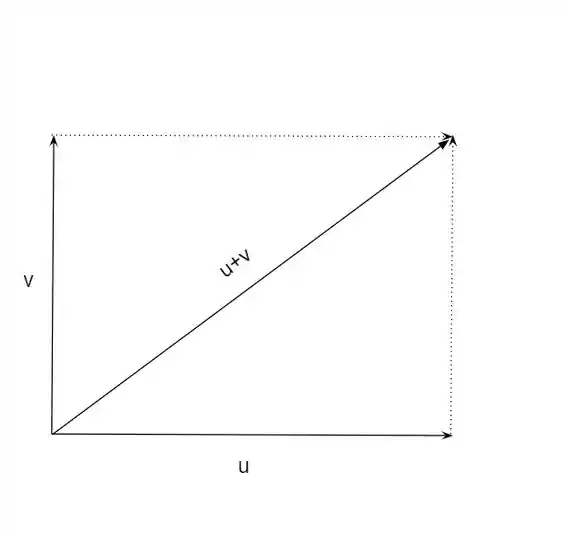
Mas sabemos que a diagonal de um quadrado de lado x é x 2 , logo u → + v → = 2 u →

Vamos agora para o segundo item.

B   S e   u → + v →   é   o r t o g o n a l   a   u → - v → ,   e n t ã o   u → = v →

Se S e   u → + v →   é   o r t o g o n a l   a   u → - v → temos u → + v →   ,   u → - v → = 0 ,   m a s :

  u → + v →   ,   u → - v → = u → , u → - v → + v → , u → - v →

u → , u → - u → , v → + v → , u → - v → , v → = 0

u → , u → = v → , v →

Logo u → = v →

Passo 2

Vamos para terceira equação:

C   S e   α   ∈ R   s a t i s f a z   α v → = 0 → ,   e n t ã o   α = 0   o u   v → = 0

Essa é bem direta, não tem muito para onde correr, mas se quiser se convencer mais podemos tomar v → = a , b , c

α a , b , c = 0,0 , 0

α a = 0 α b = 0 α c = 0

Logo α = 0   o u   a = b = c = 0

Passo 3

Agora as afirmações D, E saem na mesma, pois se u → ∙ v → = 0   temos dois casos:

Caso 1) u → = 0   o u   v → = 0

Caso 2) u → ⊥ v →

Ou seja, a letra D é verdade, pois cai no segundo caso, já a letra E é mentira, pois basta tomarmos vetores ortogonais que seu produto interno será nulo, mesmo eles não sendo nulos.

Resposta

Letra E

Exercícios de Livros Relacionados

Escreva cada combinação de vetores como um único vetor. P Q → + Q R → R P → + P S → Q S → - P S → R S → + S P → + P Q →
Ache um vetor que possui a mesma direção e o mesmo sentido que - 2,4 , 2, mas tem comprimento 6 .
Velocidades têm módulo, direção e sentido, sendo portanto vetores. O módulo de uma velocidade é chamado velocidade escalar. Suponha que esteja ventando na direção N 45 ° W a uma velocidade de 50 km/h.
Suponha que a e b sejam vetores não nulos, não paralelos e que c seja um vetor pertencente ao plano determinado por a e b . Dê um argumento geométrico para mostrar que c pode ser escrito como c = s a
Determine a + b , 2 a + 3 b , |a| e |a - b| . 18. a = 4 i + j , b = i - 2 j