Seja fixado um sistema de coordenadas no espaço, com

uma base ortonormal. Considere a quádrica de equação

e suponha que uma equação reduzida para essa quádrica seja

para um certo Sabe-se que 3 é um autovalor da matriz

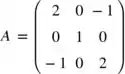
e que:

e

O valor de é:

1. 3
2. 1
3. 5
4. 2
5. 0

O enunciado diz que a equação reduzida da quádrica é:

Contudo, nossa equação original é da forma

Então como passamos de uma equação para outra?

Vamos usar a diagonalização!!!! Mas como assim???? Vem comigo!!!

Nossa quádrica pode ser reescrita na forma matricial da seguinte forma

Então se conseguíssemos escrever como uma matriz diagonal, os termos cruzados iriam desaparecer. Mas é uma matriz quadrada, simétrica, e temos seus autovalores. Logo, existe uma base onde é diagonal.

A pergunta agora é: Que base é essa? E como fica nessa nova base?

Para responder as perguntas que fizemos no passo anterior, vamos lembrar que como é diagonalizável, então

Então

Normalizando os autovetores, temos que:

com matriz diagonal onde suas entradas são os autovalores de

Tá, mas como usamos isso a nosso favor? Vamos fazer a seguinte mudança de base:

Vamos substituir isso na expressão da quádrica na forma matricial. Ela fica:

então:

Já temos todo o caminho bem definido, mas ainda precisamos calcular quem é . E para isso, precisamos do autovetor associado ao autovalor da matriz . Vamos encontrá-lo!!!

Para encontrar esse vetor, precisamos resolver o sistema

Fazendo o produto matriz vetor temos o seguinte sistema de equações:

Cuja solução é:

Prontinho, agora só precisamos desenvolver a expressão

Lembrando que é:

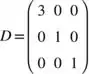
e que é:

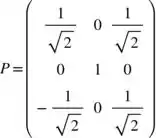
onde suas colunas são os autovetores normalizados

então

(somando e subtraindo 2 para completar os quadrados)

Com isso temos que

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊