USP – Álgebra Linear 2 – P3 – 2016
Q2. Seja uma matriz real e seja o operador linear tal que , em que can denota a base canônica de . Suponha que o polinômio característico de seja
E que
e ,
Em que denota o autovalor de que tem a parte imaginária positiva e denota o operador identidade de . Temos que a solução geral real do sistema de equações diferenciais é dada por:
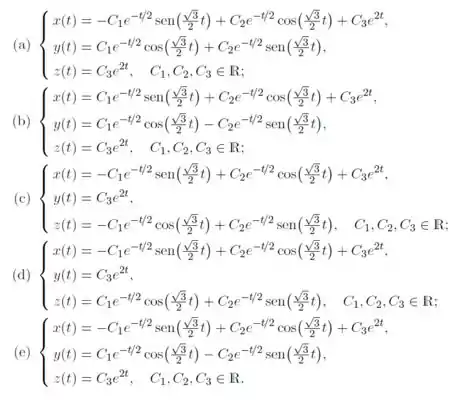
Passo 1
Falaaa... beleza???
Nessa questão vamos achar a solução da equação diferencial:
Pra isso,
Passo 2
Como temos o polinômio característico, podemos achar os autovalores:
Então:
Resposta
c
Exercícios de Livros Relacionados
Para cada sistema do Exercício 3 que for linear, determine se é consistente.
Em cada parte, determine se as equações formam um sistema linear no sistema: - 2 x + 4 y + z = 2 3 x - 2 y = 0
Na linha do exercício anterior, mostre que se a1b2 − a2b1 ≠ 0 então o sistema admite sempre uma solução do tipo (x, y, 0).
No sistema abaixo, atribua sucessivamente valores aos parâmetros m, n de modo que as três equações representem um único plano, dois planos ou três planos: x-2 y-3 z=m3 x-6 y-9 z=n- 2 x+4 y+6 z=1
Para cada um dos sistemas abaixo, decida em qual dos casos (primeiro a oitavo) discutidos no texto ele se enquadra. Determine também todas as soluções do sistema, se houver. 3 x-5 y+2 z=14 x-3 y+z=22