Seja uma matriz real e seja o operador linear tal que , em que denota a base canônica de . Denote por a identidade. Se for um autovalor de , então será igual a:
a)
b)
c)
d)
e)
Passo 1
Fala galera!!! Tudo bem com vocês? Vamos para mais uma questão de Algelin. Nosso objetivo nessa questão é calcular , e para isso o enunciado nos diz que , e que é um autovalor de ,ou seja, é um autovalor de . E como , é uma matriz 2x2.
Vamos calcular essa matriz/operador!!!
Passo 2
O enunciado está pedindo para calcularmos uma potência de uma matriz e, além disso, nos informa um dos autovalores. Então como vocês acham que eles querem que calculemos essa potência?

Isso aí! Vamos diagonalizar a matriz , isto é escrevê-la da forma
com matriz diagonal formada de autovalores de E a matriz dos autovetores
Escrevendo dessa forma conseguimos mostrar que
Que é bem mais fácil de calcular!!!
Passo 3
No passo anterior, vimos que será necessário diagonalizar para calcular . Para isso precisamos obter os autovalores de . como que obtemos esses autovalores?
Por definição, os autovalores são as raízes do polinômio característico. Esse polinômio é:
Mas espera a e, os autovalores são as RAÍZES do polinômio característico. Logo se for raiz,
também será.Dessa forma os autovalores de são:

Passo 4
Descobrimos que os autovalores de são . Vamos calcular
Como ficaria a matriz ?
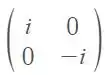
Essa é a nossa matriz , logo
é:
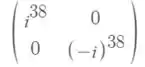
Vamos resolver essas potências de
.
Ou seja, nossa matriz
pode ser escrita como . Então
(reescrevendo D)
(colocando o sinal de menos para fora)
(usando a definição do operador identidade)

E com isso chegamos ao fim de mais uma questão de algelin 😊. Espero que os passos tenham ficado claros. Até a próxima!!!