USP, Sem Campus, Álgebra Linear 2, P3 - 2017, Questão 8
Considere o espaço vetorial munido do seu produto interno usual. Seja a transformação linear tal que
em que B é a base de dada por:
Considere as seguintes afirmações:
(I) é simétrico;
(II) possui dois autovalores distintos;
(III) ́ é diagonalizável.
Assinale a alternativa correta:
Assinale a alternativa correta:
(a) todas afirmações são necessariamente verdadeiras;
(b) apenas as afirmações (I) e (III) são necessariamente verdadeiras;
(c) apenas as afirmações (I) e (II) são necessariamente verdadeiras;
(d) apenas as afirmações (II) e (III) são necessariamente verdadeiras
(e) Todas as afirmações são falsas.
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar quais afirmações são verdadeiras. Show? Vamos nessa!!
Começando pela primeira. Ela diz que é simétrico. Bem, vamos descobrir que é , isto é, a nossa transformação na base canônica.
Bem temos que,
Como
Seja e os vetores da base lacônica de Então, pela definição de , temos:
E temos que
Passo 2
Agora podemos calcular . Como
E é
então
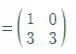
Que não é simétrica. Logo a primeira afirmação é falsa. E, ao olharmos as alternativas, vimos que isso implica que a segunda e terceira afirmações são verdadeiras. Logo a resposta é a alternativa
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
d)