USP, Sem Campus, Álgebra Linear 2, P3 - 2017, Questão 1
Seja fixado um sistema de coordenadas no plano, com
uma base ortonormal. Denote por o conjunto formado pelos números
reais a para os quais a equação
representa uma elipse. Assinale a alternativa correta:
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é descobrir qual qual a condição para para que a equação
seja uma elipse. Como vamos fazer isso? Vamos usar o processo de diagonalização de matrizes para reescrever a equação acima.
Passo 2
A primeira coisa que precisamos fazer é reescrever a nossa equação como produto de Matrizes. Então temos que
pode ser reescrita como
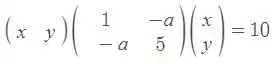
Vamos reescrever essa matriz, que chamaremos de , na sua forma diagonal, isto é, se essa matriz pode ser escrita na forma . Onde é uma matriz diagonal formada pelos autovalores de e a matriz onde as colunas são os autovetores de , onde os autovetores precisam estar na mesma ordem dos seus respectivos autovalores em .
Mas porque vamos fazer isso? Ora se
E trabalhar com matrizes diagonais é mais simples.
Então, vamos começar calculando os autovalores de . Como é:
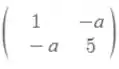
seus autovalores serão dados pelas raízes do polinômio característico
que são:
Passo 3
Bem, como comentamos no passo anterior, precisamos fazer uma mudança de base. Que base vamos tomar? Vamos dizer que
onde , é a matriz contendo os autovetores normalizados de . Fazendo isso, temos que:
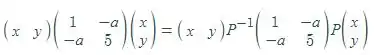
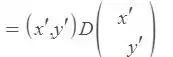
e como nossos autovalores são
Então
fazendo mais algumas manipulações chegamos que
agora, quando a equação abaixo representa uma elipse?
Para ser uma elipse, precisamos que os coeficientes que acompanham sejam positivos. Ou seja que
Como o primeiro é sempre positivo. Precisamos verificar a condição apenas no segundo coeficiente. Então temos,
isolando
elevando ao quadrado,
Logo,
Valor presente na alternativa
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
a)