USP, Sem Campus, Álgebra Linear 2, P3 - 2017, Questão 12
Considere o espaço vetorial munido do seu produto interno usual. Seja um operador linear e sejam tais que
sejam autovetores de associados, respectivamente, aos autovalores . Temos que o operador S será simétrico se, e somente se:
(a);
(b);
(c) ;
(d) ;
(e).
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar quais as condições são necessárias nos autovalores de para que seja simétrica. Show? Vamos nessa!!
Como sabemos os autovalores e autovetores de temos que:
Onde é uma matriz diagonal formada pelos autovalores de e a matriz onde as colunas são os autovetores de , onde os autovetores precisam estar na mesma ordem dos seus respectivos autovalores em .
E como queremos que seja simétrica, precisamos que
Então fazendo as contas temos que:
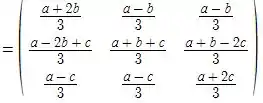
Passo 2
No passo anterior, chegamos a conclusão que é:
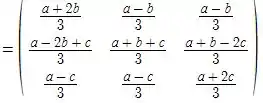
Logo para ser simétrico, precisamos que
Da segunda equação temos que:
da terceira equação, temos que
da primeira equação, também chegamos a conclusão que
Logo, a condição necessária para ser simétrica é que está na letra
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima quest��o e bons estudos!!!! 😊
Resposta
c)