Exercícios Resolvidos de Espaços Vetoriais

Ver Teoria

Exercício 6 1 2 3 4 5 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54

Enunciado

USP, Sem Campus, Álgebra Linear 2, P3 - 2017, Questão 16

Seja

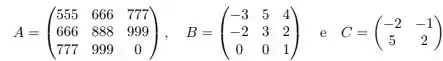
Assinale a alternativa correta:

(a) nem e nem são diagonalizáveis sobre os complexos e é diagonalizável sobre os complexos, mas não sobre ;

(b) é diagonalizável sobre e são diagonalizáveis sobre os complexos , mas

nem e nem são diagonalizáveis sobre ;

(c) são diagonalizáveis sobre R;

(d) são diagonalizáveis sobre e é diagonalizável sobre os complexos, mas não sobre ;

(e) são diagonalizáveis sobre os complexos, mas nenhuma delas é diagonalizável sobre .

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin sobre diagonalização. Nosso objetivo é verificar qual afirmação é verdadeira. Show? Vamos nessa!!

Vamos começar verificando os autovalores de cada matriz. Começando pela matriz .

Como é simétrica com coeficientes reais, o teorema espectral garante a sua diagonalização sobre . Logo é diagonalizável. Agora, vamos para as matrizes

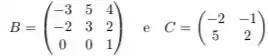
Vamos calcular os autovalores de . Por definição, são as raízes do polinômio característico definido por

cujas raízes são:

Logo é diagonalizável sobre os complexos, mas não é sobre , uma vez que seus autovalores são complexos.

Passo 2

Por fim, podemos calcular os autovalores de . Seu polinômio característico é

cujas raízes são:

E como temos três autovalores distintos é diagonalizável sobre os complexos, mas não é sobre , uma vez que seus autovalores são complexos.

Logo a alternativa é a correta

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Exercícios de Livros Relacionados

Verifique se são espaços vetoriais os seguintes conjuntos:a) O R 2 com a adição usual e a multiplicação por escalar definida por α x , y = α x , 0 . b) O R 2 com x 1 , y 1 + x 2 , y 2 = ( x 1 + 2 x 2

Sejam X um conjunto não vazio e V um espaço vetorial. Mostre que, com as definições naturais de soma e multiplicação por escalar de funções, o conjunto das funções de X em V , F (X; V ), é um espaço v

Nos exercícios 5-6, em cada parte esboce, com ponto incial na origem, o vetor determinado pelos dois pontos dados.6 (a) P1(-1,0,2), P2(0,-1,0)

34 Seja P o ponto 1 ,3 ,7 . Se o ponto 4 ,0 ,- 6 for o ponto médio do segmento de reta que liga P e Q, quem é Q?

O problema apresenta um conjunto com as operações de adição e multiplicação por escalar nele definida. Verificar se é um espaço vetorial, e se não for, cite os axiomas que não se verificam. A = 0 a b