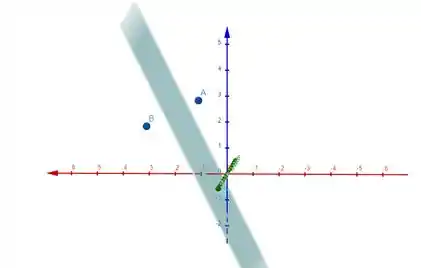
Considere os pontos e . Determine uma equação para o lugar geométrico dos pontos que são equidistantes de e .
Passo 1
Vamos chamar de um ponto genérico .
A distância de até o ponto é
A distância de até o ponto é
Queremos que tenha a mesma distância até e até , então precisamos fazer tendeu?
Passo 2
Vamos igualar as distâncias:
Abrindo os quadrados:
Esse é o plano mediador do segmento .
Vamos ver um esboço do plano com os pontos equidistantes pra ficar mais claro:
Resposta
Exercícios de Livros Relacionados
Determine a equação do plano que passa pelo ponto ( 4 ,0 ,- 3 ) e cujo vetor normal é j + 2 k .
Determine a equação do plano que passa pela origem e é paralelo ao plano 2 x - y + 3 z = 1 .
Determine as equações paramétricas da reta que passa pelo ponto ( 0 , 1,2 ) , é perpendicular à reta x = 1 + t , y = 1 - t , z = 2 t , e intercepta essa reta.
Quais das quatro retas seguintes são paralelos? Existem duas coincidentes? L 1 : x = 1 + t ,y = t ,z = 2 - 5 t L 2 : x + 1 = y - 2 = 1 - z L 3 :x = 1 + t ,y =4 + t ,z = 1 - t L 4 : r → = 2,1 , - 3 + t
Quais dos quatro planos seguintes são paralelos? Existem dois coincidentes? P 1 : 4 x - 2 y + 6 z = 3 P 2 : 4 x - 2 y - 2 z = 6 P 3 :- 6 x + 3 y - 9 z = 5 P 4 : z = 2 x - y - 3