Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução ao Plano

Ver Teoria
Exercício 91234567810111213141516171819202122

Enunciado

Escreva equações paramétricas para os três planos coordenados.

Passo 1

O exercício pede para escrevermos as equações paramétricas dos três planos coordenados. Mas, quais são esses planos ??

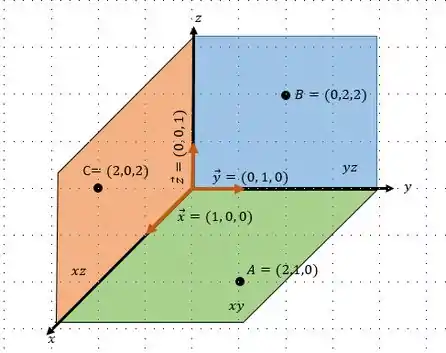
Você já os conhece!! Talvez, não esteja lembrando!! Os três planos coordenados, são os planos x y ,   x z e y z , como mostra a figura a seguir:

Passo 2

Vamos começar analisando o plano x y !

Pela figura o plano x y é o verde. Podemos ver que na figura já desenhamos dois vetores paralelos ao plano x y que são os vetores x → = ( 1 ,   0 ,   0 ) e y → = ( 0,1 ,   0 ) . Poderíamos ter escolhido qualquer outro vetor que pertencesse ao plano. E escolhemos também um ponto qualquer pertencente ao plano que no caso é o ponto A = ( 2 ,   1 ,   0 ) . Já temos dois vetores paralelos ao plano x y e um ponto pertencente ao plano, agora é só colocar os valores nos lugares adequadas da forma paramétrica, que é:

x =   x 1 + λ v 1 + µ u 1 y =   y 1 + λ v 2 + µ u 2 z =   z 1 + λ v 3 + µ u 3

Sabemos, pela teoria que x 1 ,   y 1 ,   z 1 são as coordenadas do ponto pertencente ao plano, no nosso caso é A = ( 2 ,   1 ,   0 ) . Já as coordenadas v 1 ,   v 2 ,   v 3 e u 1 ,   u 2 ,   u 3 são as coordenadas dos vetores paralelos ao plano x y , então podemos dizer que:

v 1 ,   v 2 ,   v 3 = x → = ( 1 ,   0 ,   0 )

u 1 ,   u 2 ,   u 3 = y → = ( 0,1 ,   0 )

x 1 ,   y 1 ,   z 1 = A = ( 2 ,   1 ,   0 )

Escrevendo na forma paramétrica, temos:

x =   2 + λ 1 + µ 0 y =   1 + λ 0 + µ 1 z =   0 + λ 0 + µ 0 →   x =   2 + λ y =   1 + µ z =   0  

Passo 3

Vamos fazer agora para o plano x z que está em laranja. O procedimento é o mesmo o que vai mudar é o ponto pertencente ao plano e os vetores paralelos. Os vetores e o ponto são:

x → = 1 ,   0 ,   0 = v 1 ,   v 2 ,   v 3

z → = 0 ,   0 ,   1 = u 1 ,   u 2 ,   u 3

C = 2 ,   0 ,   2 = x 1 ,   y 1 ,   z 1

Colocando na forma paramétrica teremos:

x =   2 + λ 1 + µ 0 y =   0 + λ 0 + µ 0 z =   2 + λ 0 + µ 1 →   x =   2 + λ y = 0 z =   2 + µ  

Passo 4

Para terminar vamos montar as equações paramétricas do plano y z . Pela figura o ponto escolhido e os vetores são:

y → = 0 ,   1 ,   0 = v 1 ,   v 2 ,   v 3

z → = 0 ,   0 ,   1 = u 1 ,   u 2 ,   u 3

B = 0 ,   2 ,   2 = x 1 ,   y 1 ,   z 1

Substituindo nas equações paramétricas, temos:

x =   0 + λ 0 + µ 0 y =   2 + λ 1 + µ 0 z =   2 + λ 0 + µ 1 →   x =   0 y =   2 + λ z =   2 + µ  

Lembrando, que poderíamos ter escolhido outros pontos e vetores. Os vetores que escolhemos são os mais simples para serem utilizados, já os pontos poderíamos ter escolhidos pontos que estivessem sobre os eixos coordenados, porque assim mais coordenadas seriam ZERO e facilitaria nossas contas!!

Resposta

Equações Paramétricas do Plano x y :

x =   2 + λ y =   1 + µ z =   0  

Equações Paramétricas do Plano x z :

x =   2 + λ y = 0 z =   2 + µ  

Equações Paramétricas do Plano y z :

x =   0 y =   2 + λ z =   2 + µ  

Exercícios de Livros Relacionados

Determine a equação do plano que passa pelo ponto ( 4 ,0 ,- 3 ) e cujo vetor normal é j + 2 k .
Determine a equação do plano que passa pela origem e é paralelo ao plano 2 x - y + 3 z = 1 .
Determine as equações paramétricas da reta que passa pelo ponto ( 0 , 1,2 ) , é perpendicular à reta x = 1 + t , y = 1 - t , z = 2 t , e intercepta essa reta.
Quais das quatro retas seguintes são paralelos? Existem duas coincidentes? L 1 : x = 1 + t ,y = t ,z = 2 - 5 t L 2 : x + 1 = y - 2 = 1 - z L 3 :x = 1 + t ,y =4 + t ,z = 1 - t L 4 : r → = 2,1 , - 3 + t
Quais dos quatro planos seguintes são paralelos? Existem dois coincidentes? P 1 : 4 x - 2 y + 6 z = 3 P 2 : 4 x - 2 y - 2 z = 6 P 3 :- 6 x + 3 y - 9 z = 5 P 4 : z = 2 x - y - 3