Determinar as equações paramétricas da reta interseção dos planos:
e
Passo 1
Num dos exercícios anteriores determinamos o ponto de interseção entre uma reta e um plano. Agora, queremos determinar a reta que é formada por meio da intereseção entre os planos e . Esse tipo de exercício tem duas formas básicas de resolução!! Vamos fazer as duas passo a passo para você entender direitinho e ver qual prefere para resolver!!

Passo 2
Vamos começar!!!
Primeira maneira:
Sabemos que a reta interseção ela deve satisfazer as duas equações dos planos, então teremos um sistema de equações:
Com essas duas equações podemos determinar as equações reduzidas da reta interseção. Para isso, vamos escrever as equações em função de . Assim, vamos somar as duas equações, para obter o em função de e depois multiplicar a equação por e somar com a equação para obter em função de Fazendo essas manipulações, teremos:
Com essas equações sabemos que os pontos da reta interseção são:
Tendo o ponto genérico da reta, conseguimos determinar a reta sabendo dois pontos dela. Assim,
Um vetor diretor da reta possível é:
E escolhendo, um dos pontos ou , nos caso escolheremos . Conseguimos escrever as equações paramétricas da reta:
Então as equações paramétricas da reta interseção dos dois planos é:
Passo 3
Segunda maneira:
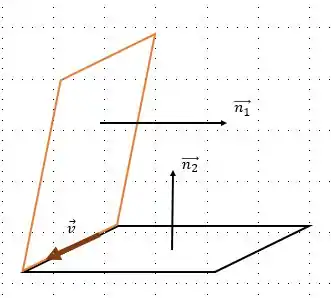
Se nós temos o vetor normal de cada um dos planos, e sabendo que o vetor diretor da reta da interseção é perpendicular entre os dois vetores normais, isso está me lembrando uma coisa!!! Para achar um vetor que seja normal à outros dois fazemos o produto vetorial entre o vetores normais e então encontraremos o vetor . Assim, faremos:
Assim, pelas equações gerais acharemos e :
e
Agora, basta montarmos e resolvermos o produto vetorial: 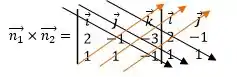
Já sabemos o vetor diretor da reta, agora só falta descobrirmos um ponto pertencente à reta. Para isso vamos usar as duas equações dos planos:
Se a reta deve satisfazer essas duas equações, então se chutarmos pontos que satisfaçam às equações então elas pertencem à reta:
Somando as duas equações, temos:
Para descobrir basta substituirmos em alguma das duas equações, vou escolher a primeira:
Portanto, um ponto que pertence à reta é:
Então, sabendo que o vetor diretor é e o ponto , podemos escrever as equações paramétricas da reta interseção:
Se você notar, o vetor diretor que achamos é o mesmo que encontramos com a primeira forma, porém multiplicado por .