Estabelecer a equação geral do plano determinado pelos pontos e .
Passo 1
Esse problema é parecido com o anterior que fizemos, pois o exercício nos pede novamente a equação geral do plano. Porém, o enunciado nos fornece 3 pontos que determinam o plano que queremos. Que estanho!! Como faço isso tendo apenas 3 pontos? Na teoria não lembro de ter visto nada disso!! Realmente, você ainda não viu!! Mas, você vai ver como é possível fazer isso!!

Passo 2
Vamos analisar a figura a seguir
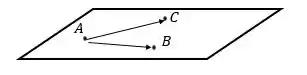
Com os três pontos e pertencentes ao plano conseguimos formar dois vetores que sejam paralelos ao plano, por exemplo, os vetores e . Assim, teríamos dois vetores paralelos ao plano e ainda podemos escolher um dos 3 pontos para achar a equação geral do plano fazendo o produto misto.
Então, vamos primeiro calcular os vetores e .
Passo 3
Agora, já temos dois vetores paralelos ao plano e não são paralelos entre si. Falta escolher um ponto para fazer o produto misto. Porquê eu quero vou escolher o ponto . Então, bora montar o produto misto. Lembrando que o terceiro vetor é formado pelo ponto e o ponto genérico que gera .
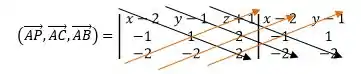
Para tornar os índices os mais reduzidos podemos multiplicar por e obteremos:
Prontinho, chegamos na equação geral. Lembrando que os vetores paralelos poderiam ter sido outros que o resultado daria no mesmo, bem como o ponto escolhido.
Ainda, há uma segunda forma de se resolver esse problema que é ao invés de zerar o produto misto, poderíamos fazer o produto vetorial entre os vetores paralelos ao plano encontrados e assim acharíamos o vetor normal ao plano. Escolheríamos um ponto e substituiríamos direto na equação geral do plano .