Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução ao Plano

Ver Teoria
Exercício 17123456789101112131415161819202122

Enunciado

Na figura são dadas as retas

r : X = 0 ,   2 ,   1 + λ ( 1 ,   1 ,   1 )

s : x + 1 = y - 1 = z + 2 3

E o plano π : 2 x - y + z - 1 = 0 . Determine as coordenadas dos pontos A , B e C .

Passo 1

Olha só, esse é um exercício que vamos trabalhar bastante com intersecções :D

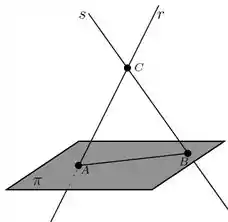
Queremos os pontos A , B e C , e observando a figura do enunciado temos que

  • A é a intersecção da reta r com o plano π ( A = r ∩ π )
  • B é a intersecção da reta s com o plano π ( B = s ∩ π )
  • C é a intersecção da reta r com a reta s ( B = r ∩ s )

Então vamos encontrar essas intersecções fechou?

Passo 2

Vamos começar pelo ponto A . Um ponto genérico da reta r é A = ( λ ,   2 + λ ,   1 + λ ) , vamos substituir esse ponto na equação do plano π pra encontrarmos o λ que satisfaz essa intersecção:

2 x - y + z - 1 = 0

2 λ - 2 + λ + ( 1 + λ ) - 1 = 0

2 λ - 2 = 0

λ = 1

Substituindo esse λ no ponto A , temos que

A = ( 1 ,   3 ,   2 )

Passo 3

Antes de encontrarmos o ponto B , vamos escrever a equação da reta s de forma paramétrica:

s :   t = x + 1 = y - 1 = z + 2 3

s :   t = x + 1 t = y - 1 t = z + 2 3

s :   x = - 1 + t y = 1 + t z = - 2 + 3 t

Beleza, temos que um ponto genérico da reta s é B = ( - 1 + t ,   1 + t ,   - 2 + 3 t ) . Substituindo esse ponto na equação do plano π :

2 x - y + z - 1 = 0

2 - 1 + t - 1 + t + - 2 + 3 t - 1 = 0

4 t - 6 = 0

t = 6 4 = 3 2

Boaa, substituindo o valor de t no ponto B :

B = 1 2 , 5 2 , 5 2

Passo 4

Pra acharmos a intersecção de r e s , os seus pontos genéricos devem ser iguais:

λ = - 1 + t 2 + λ = 1 + t 1 + λ = - 2 + 3 t

Substituindo a primeira linha na terceira:

1 - 1 + t = - 2 + 3 t

2 t = 2

t = 1

Substituindo esse valor de t no ponto genérico da reta s , temos

C = - 1 + t ,   1 + t ,   - 2 + 3 t = ( 0 ,   2 ,   1 )

E fimmm!!

Resposta

A = ( 1 ,   3 ,   2 )

B = 1 2 , 5 2 , 5 2

C = ( 0 ,   2 ,   1 )

Exercícios de Livros Relacionados

Determine a equação do plano que passa pelo ponto ( 4 ,0 ,- 3 ) e cujo vetor normal é j + 2 k .
Determine a equação do plano que passa pela origem e é paralelo ao plano 2 x - y + 3 z = 1 .
Determine as equações paramétricas da reta que passa pelo ponto ( 0 , 1,2 ) , é perpendicular à reta x = 1 + t , y = 1 - t , z = 2 t , e intercepta essa reta.
Quais das quatro retas seguintes são paralelos? Existem duas coincidentes? L 1 : x = 1 + t ,y = t ,z = 2 - 5 t L 2 : x + 1 = y - 2 = 1 - z L 3 :x = 1 + t ,y =4 + t ,z = 1 - t L 4 : r → = 2,1 , - 3 + t
Quais dos quatro planos seguintes são paralelos? Existem dois coincidentes? P 1 : 4 x - 2 y + 6 z = 3 P 2 : 4 x - 2 y - 2 z = 6 P 3 :- 6 x + 3 y - 9 z = 5 P 4 : z = 2 x - y - 3