Um plano em divide o espaço em duas partes, denominadas semiespaços. Considere o plano Qual dos seguintes pontos encontra-se no mesmo semiespaço que o ponto
(a)
(b)
(c)
(d)
Passo 1
Beleza, como a questão disse, um plano do divide o espaço em dois semiespaços.
Pra visualizar isso lembra do plano do .
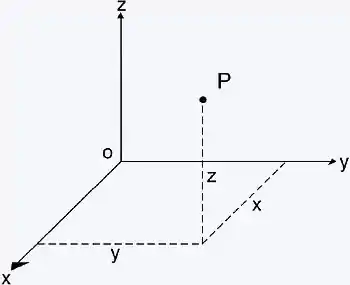
Todos os pontos desse plano têm coordenada z igual a 0.
Os pontos acima dele tem coordenadas z positiva e os pontos abaixo tem z negativo, certo??
Então vamos pensar no nosso plano como se fosse o plano xy dividindo o espaço em uma região positiva e outra negativa.
Passo 2
Pra ver de qual lado do plano um ponto está, vamos substituir as coordenadas dele na equação do plano e avaliar se o resultado é positivo ou negativo.
Bora fazer isso pro ponto que foi dado no enunciado, que foi o
Opa, então vamos procurar nas alternativas um cara tal que, quando substituímos as coordenadas dele na equação do plano dado, o resultado também dê um número positivo.
Fazendo alternativa por alternativa:
(a)
(b)
(c)
(d)
Nota que o ponto da letra (c) foi o único que também deu positivo.
Então ele é o único que tá do mesmo lado do plano dado e vai ser a nossa resposta.
Resposta
(c)