Forças e Torque sobre uma Espira
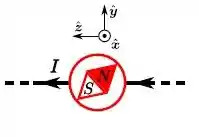
Uma bússola encontra-se acima de um fio retilíneo, muito longo, percorrido por uma corrente elétrica estacionária de intensidade . Na sua posição de equilíbrio estável, quais são o sentido do vetor momento de dipolo magnético da bússola e a sua energia potencial , supondo que esta última é zero quando .
- e
- e
- e
- e
- e
- e
Passo 1
O sentido do momento de dipolo de um imã é do Sul pro Norte. O torque é dado por:
Sabemos que o campo gira em torno do fio. Utilizando a regra da mão direita, coloque o polegar no sentido da corrente que os outros dedos dão o sentido do campo.
Como a bússola está acima, podemos visualizar o campo vendo a figura de lado:
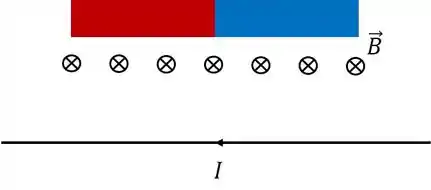
Passo 2
Logo, o sentido do campo é . O equilíbrio é atingido quando não há torque:
Que é quando o campo e o momento de dipolos são paralelos.
Passo 3
O equilíbrio é estável quando a energia potencial é mínima. A energia potencial tem fórmula:
Que equivale a:
Este valor é mínimo para :
Portanto é quando o e o apontam no mesmo sentido, ao invés de sentidos opostos. Por consequência, o sentido de é e o valor da energia é , conforme calculado.
Resposta
Letra a