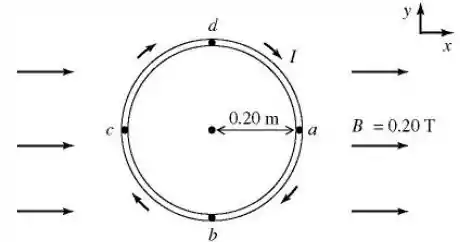
A figura ilustra uma espira circular de raio na qual circula uma corrente elétrica no sentido horário. A espira situa-se no plano e um campo magnético uniforme externo de magnitude aponta na direção positiva do eixo , como ilustrado.
A magnitude do momento de dipolo magnético da espira é .
Se a espira for liberada, a partir do repouso, da configuração mostrada na figura, seu movimento devido ao torque magnético é tal que (considere os 4 pontos representados na espira, rotulados de a , b , c e d ):
a espira não se moverá, pois está em uma configuração de equilíbrio estável.
ponto a move-se para fora da página e ponto move-se para dentro da página.
ponto a move-se para dentro da página e ponto move-se para fora da página.
ponto b move-se para fora da página e ponto move-se para dentro da página.
ponto b move-se para dentro da página e ponto move-se para fora da página.
Passo 1
O torque magnético é dado por:
O sentido do momento de dipolo magnético é determinado pela regra da mão direita, indicado pelo polegar, onde os outros dedos seguem o sentido da corrente na espira. Nesse caso, o vetor está entrando no plano da página.
Utilizando novamente a regra da mão direita para o produto vetorial, o dedo indicador irá representar o vetor , enquanto o vetor será representado pelo dedo médio, com o polegar indicando o sentido do vetor resultante.
Nesse caso, o torque magnético está apontando para baixo, fazendo com que o ponto a se mova para fora da página e ponto se mova para dentro da página.
A resposta certa é a letra .
Resposta
ponto a move-se para fora da página e ponto move-se para dentro da página.