Uma espira quadrada, de arestas de comprimento , pela qual flui uma corrente estacionária de intensidade , está no plano , com dois de seus lados paralelos ao eixo , como mostrado na figura abaixo.
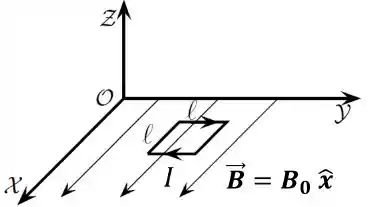
A corrente na espira flui no sentido horário para um observador localizado no semi-eixo positivo . Na região onde a espira se encontra há um campo magnético constante (estacionário e uniforme) .
O torque sobre a espira é dado por:
;
;
;
;
;
;
;
Nulo;
Passo 1
O torque magnético sobre uma espira é dado por:
O vetor momento de dipolo magnético é dado por:
Onde o módulo de é igual à área da espira, e sua direção e sentido são determinados pela regra da mão direita, onde todos os seus dedos (exceto o polegar) ficam na mesma direção e sentido da corrente elétrica, e o seu polegar irá apontar o sentido do vetor .
Fazendo isso, concluímos que o vetor está no sentido , logo:
Passo 2
Finalmente, o torque magnético será dado por:
A resposta correta é a letra .
Resposta
;