UFRJ- Física 3 – PF 2018.2 - DIURNO - 9
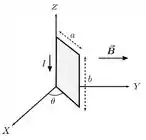
Uma espira condutora retangular de lados e é posicionada sobre um sistema de coordenadas como mostrado na figura abaixo. Um de seus lados está sobre o eixo e o seu plano forma um ângulo com o plano . Ela transporta uma corrente estacionária de intensidade , no sentido indicado, e encontra-se sob a ação de um campo magnético constante , também indicado na figura. Nessas condições, o torque que o campo magnético exerce sobre a espira vale:
Passo 1
Se olhamos a espira a partir do eixo , vemos a corrente percorrendo a espira no sentido anti-horário. Nesse caso, pela regra da mão direita, o vetor área , que é perpendicular à superfície, aponta na direção e sentidos dados por
em que é o seu módulo.
Passo 2
Agora, para calcular o vetor torque, precisamos realizar o seguinte produto vetorial
sendo que e . Como , o torque vai ficar escrito como
Resposta
Letra a).