Na figura abaixo o campo magnético é uniforme e perpendicular ao plano da figura, apontando para fora (direção positiva do eixo ). A espira é formada por um quarto de círculo de raio (arco ) e por dois segmentos retilíneos e de comprimento , conforme-te a figura. Pela espira circula uma corrente no sentido anti-horário.
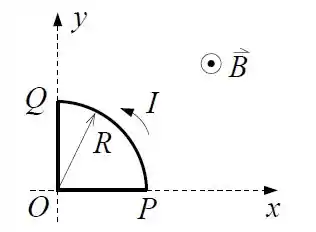
Calcule o torque que age sobre a espira.
Passo 1
Calcule o torque que age sobre a espira.
O torque sobre uma espira é dado por:
Onde é o momento dipolar magnético, dado por:
Logo, o torque sobre a espira será:
Resposta
Exercícios de Livros Relacionados
Uma esfera uniforme, sólida, uniformemente carregada, de raio R , tem uma densidade volumétrica de carga ρ . A esfera gira em torno de um eixo que passa pelo seu centro com rapidez angular ω . Determi
Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo 2,30 A · m 2 . (b) Determine o valor máximo do torque a que a bo
Uma espira circular com 8,0 cm de raio é percorrida por uma corrente de 0,20 A . Um vetor de comprimento unitário, paralelo ao momento dipolar μ → da espira, é dado por 0,60 i ^ – 0,80 j ^ . (Esse vet
Na Fig. 28-50a, duas espiras concêntricas, situadas no mesmo plano, são percorridas por correntes em sentidos contrários. A corrente i 1 na bobina 1 é fixa e a corrente i 2 na bobina 2 é variável. A F
A bobina da Fig. 28-49 conduz uma corrente i = 2,00 A no sentido indicado, é paralela ao plano x z , possui 3,00 espiras, tem uma área de 4,00 × 10 - 3 m 2 e está submetida a um campo magnético unifor