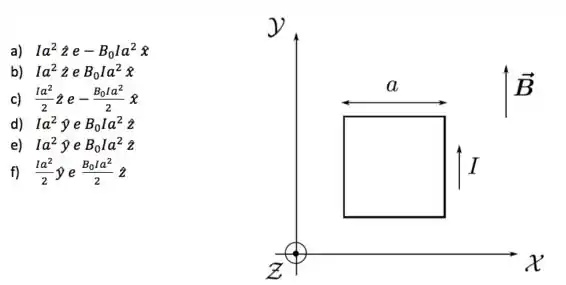
Uma espira condutora quadrada de lado é posicionada sobre o plano de um sistema de coordenadas, como mostrado na figura abaixo. Uma corrente estacionária de intensidade circula a espira no sentido indicado. Ela está imersa em uma região de campo magnético estacionário e uniforme dado por  , onde é uma constante positiva. Nessa situação, o momento de dipolo magnético da espira e o torque magnético sobre ela valem, respectivamente:

Podemos associar à essa espira condutora percorrida por uma corrente estacionária um momento de dipolo magnético  . A expressão de   é dada por

em que   é o vetor área associado à espira. O sentido e direção de   é dado pela regra da mão direita. Então, como a corrente está circulando no sentido anti-horário na figura, o vetor área é

apontando para fora do plano da página. Portanto, o momento de dipolo magnético é