(A)
(B)
(C)
(D)
(E)
Passo 1
Todas as alternativas fazem exatamente a mesma coisa que a lei de Gauss, só que com o campo magnético: calculam o fluxo em uma superfície fechada para esse tipo de campo.
Se esse fluxo for diferente de zero, isso significa que dentro da gaussiana existiria um análogo à carga: o monopólio magnético.
Acontece que, na natureza, isso não existe! É impossível existir um polo norte de imã sem um polo sul, ou vice-versa. Os dois polos de um imã sempre estão juntinhos.
Nem quebrando o imã em dois você consegue mudar essa realidade, como podemos ver na figura.
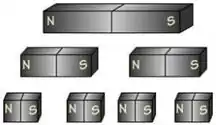
Então o fluxo magnético em uma gaussiana fechada é necessariamente zero e isso se resume à seguinte frase: não existem monopólios magnéticos.
Resposta
Letra (A).
Exercícios de Livros Relacionados
Uma esfera uniforme, sólida, uniformemente carregada, de raio R , tem uma densidade volumétrica de carga ρ . A esfera gira em torno de um eixo que passa pelo seu centro com rapidez angular ω . Determi
Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo 2,30 A · m 2 . (b) Determine o valor máximo do torque a que a bo
Uma espira circular com 8,0 cm de raio é percorrida por uma corrente de 0,20 A . Um vetor de comprimento unitário, paralelo ao momento dipolar μ → da espira, é dado por 0,60 i ^ – 0,80 j ^ . (Esse vet
Na Fig. 28-50a, duas espiras concêntricas, situadas no mesmo plano, são percorridas por correntes em sentidos contrários. A corrente i 1 na bobina 1 é fixa e a corrente i 2 na bobina 2 é variável. A F
A bobina da Fig. 28-49 conduz uma corrente i = 2,00 A no sentido indicado, é paralela ao plano x z , possui 3,00 espiras, tem uma área de 4,00 × 10 - 3 m 2 e está submetida a um campo magnético unifor