A espira retangular da figura abaixo está colocada no plano em um campo magnético:
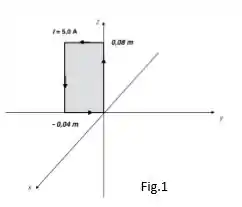
Na espira circula uma corrente com o sentido indicado na figura.
(a) Calcule o vetor momento magnético associado a essa espira.
(b) Calcule o vetor torque exercido pelo vetor campo magnético sobre a espira.
(c) Em seguida a espira é girada em torno do eixo no sentido anti-horário e colocada a (ver figura ). Calcule o vetor torque na espira nesta posição.
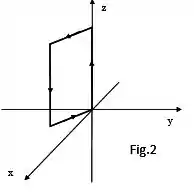
Passo 1
(a) A expressão que nos levará ao momento magnético é:
Como o vetor área, que é perpendicular ao plano da espira, está paralelo ao eixo :
Portanto, substituindo os valores de corrente e área:
Logo:
Passo 2
(b) Para encontrar o torque em relação a , usaremos que:
Substituindo os valores:
Realizando o produto vetorial:
Então:
Passo 3
(c) agora está no sentido , certo? Portanto, ele está paralelo a . O que nos leva a:
Resposta
a)
b)
c)