UFRJ – Física 3 – 2019.2 – 2º CH
. Considere a espira condutora mostrada na figura abaixo. Ela é formada pela junção de dois trechos semicirculares de raios e com dois trechos retilíneos e conduz uma corrente estacionária de intensidade no sentido indicado.
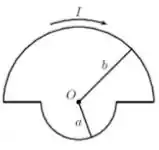
Determine o vetor momento de dipolo magnético da espira.
Passo 1
Vamos detonar com esse problema juntos!
Para encontrar o momento de dipolo magnético da espira temos que usar o fato de que o momento é dado por:
Onde é a corrente que passa pela espira e a área da espira. Então temos que encontrar essa área, mãos à obra!
Passo 2
Para encontrar a área da espira vamos usar o fato de que ela é composta por metade de uma circunferência de raio e metade de uma com raio .
A área de um círculo é dada por:
Então a metade é
Então a área da espira é:
Assim o momento de dipolo é dado por:
Para saber a direção e o sentido desse vetor basta usar a regra da mão direita levando em conta o sentido da corrente, como ela está no sentido horário esse vetor aponta para dentro da página.