Ordene os módulos dos torques que agem nas espiras circulares , e que aparecem na figura, do maior para o menor. As três espiras são idênticas e transportam correntes iguais.
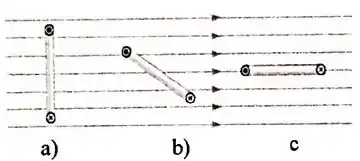
a, b, c;
a, c, b;
c, a, b;
c, b, a;
b, c, a;
Passo 1
O torque magnético sobre uma espira é dada por:
Onde tem a mesma direção e sentido do vetor área da espira, sempre perpendicular ao plano da espira.
Como queremos avaliar o módulo do torque magnético, podemos escrever o mesmo da seguinte forma:
Onde é o ângulo formado entre os vetores e .
Dessa forma, basta analisar o ângulo para cada situação.
Passo 2
Posicionando o vetor momento de dipolo magnético em cada espira, teremos:
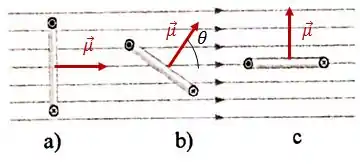
No primeiro caso, , logo:
No segundo caso, , logo:
No terceiro caso, , logo:
Finalmente:
Resposta
c, b, a;
Exercícios de Livros Relacionados
Uma esfera uniforme, sólida, uniformemente carregada, de raio R , tem uma densidade volumétrica de carga ρ . A esfera gira em torno de um eixo que passa pelo seu centro com rapidez angular ω . Determi
Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo 2,30 A · m 2 . (b) Determine o valor máximo do torque a que a bo
Uma espira circular com 8,0 cm de raio é percorrida por uma corrente de 0,20 A . Um vetor de comprimento unitário, paralelo ao momento dipolar μ → da espira, é dado por 0,60 i ^ – 0,80 j ^ . (Esse vet
Na Fig. 28-50a, duas espiras concêntricas, situadas no mesmo plano, são percorridas por correntes em sentidos contrários. A corrente i 1 na bobina 1 é fixa e a corrente i 2 na bobina 2 é variável. A F
A bobina da Fig. 28-49 conduz uma corrente i = 2,00 A no sentido indicado, é paralela ao plano x z , possui 3,00 espiras, tem uma área de 4,00 × 10 - 3 m 2 e está submetida a um campo magnético unifor