Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Magnético Dipolar

Ver Teoria
Exercício 371234567891011121314151617181920212223242526272829303132333435363839

Enunciado

UFRJ- Física 3 – P2 2018.1 - DIURNO - 2

Um nêutron é formado por três partículas elementares conhecidas como quarks. Um deles é um quark up, com carga + 2 3 e e os outros dois são quarks down, cada um com carga - 1 3 e   . Em um modelo simplificado para a estrutura interna do nêutron, os três quarks realizam movimentos circulares de mesma velocidade escalar v e raio R , todos executados no mesmo plano. O quark up gira em sentido anti-horário e os quarks down giram em sentido horário, como vistos por um mesmo observador. Nessas condições, supondo que as correntes elétricas associadas ao movimento de cada quark podem ser tratadas como correntes estacionárias, a intensidade do momento de dipolo magnético total do nêutron vale:

  1. 0
  2. 1 3   e v R
  3. 1 2   e v R
  4. 2 3   e v R
  5. e v R  
  6. 3 2 e v R
  7. 2 e v R
  8. 3   e v R

Passo 1

Sabemos que o módulo do momento de dipolo magnético é dado por

μ = I A ,

sendo que I é a corrente elétrica que passa em uma espira de área A

Tomamos a corrente como sendo o fluxo das cargas positivas. Por isso, tanto para a carga positiva + 2 3 e   do quark up, quanto para as cargas negativas – e 3   de cada uma dos quarks down, a corrente elétrica associada estará no sentido anti-horário, como mostra a Figura abaixo. Por isso, precisamos calcular o momento de dipolo magnético associado ao quark up e à carga negativa dos quarks down.

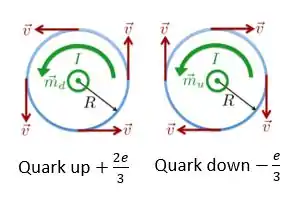
Passo 2

Para o quark up na órbita circular, a área da espira é A = π R 2 . Para encontrarmos a corrente associada ao movimento dessa carga positiva, temos que lembrar que o período orbital T é dado por

T = 2 π R v     .

A corrente equivalente é a carga total que passa em qualquer ponto da órbita por unidade de tempo, que é exatamente a carga + 2 e 3 do quark up dividida pelo período orbital T

I u = 2 e 3 T = 2 e v 6 π R ⇒ I u = e v 3 π R   .

Portanto, o módulo do momento de dipolo magnético é

μ u = I u A = e v 3 π R     π R 2 ⇒ μ u = e v R 3   .

Passo 3

A carga negativa dos quarks down, que é igual - e / 3 , e como temos dois quarks down a corrente será dada por

I d = 2 × e 3 T = 2 e 3 2 π R v = e v 3 π R = I u   .

Por isso, o momento de dipolo magnético associado à corrente I u será também dado por

μ d = e v R 3 = μ u   .

Passo 4

Como as duas correntes têm mesmo sentido, o momento magnético associado também terá a mesma direção. Por isso, o módulo do momento de dipolo magnético total associado ao nêutron nesse modelo será igual a

μ t o t a l = μ u + μ d = 2 e v R 3   .

Resposta

Letra d).

Exercícios de Livros Relacionados

Uma esfera uniforme, sólida, uniformemente carregada, de raio R , tem uma densidade volumétrica de carga ρ . A esfera gira em torno de um eixo que passa pelo seu centro com rapidez angular ω . Determi
Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo 2,30 A · m 2 . (b) Determine o valor máximo do torque a que a bo
Uma espira circular com 8,0 cm de raio é percorrida por uma corrente de 0,20 A . Um vetor de comprimento unitário, paralelo ao momento dipolar μ → da espira, é dado por 0,60 i ^ – 0,80 j ^ . (Esse vet
Na Fig. 28-50a, duas espiras concêntricas, situadas no mesmo plano, são percorridas por correntes em sentidos contrários. A corrente i 1 na bobina 1 é fixa e a corrente i 2 na bobina 2 é variável. A F
A bobina da Fig. 28-49 conduz uma corrente i = 2,00 A no sentido indicado, é paralela ao plano x z , possui 3,00 espiras, tem uma área de 4,00 × 10 - 3 m 2 e está submetida a um campo magnético unifor