Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Magnético Dipolar

Ver Teoria
Exercício 271234567891011121314151617181920212223242526282930313233343536373839

Enunciado

A figura mostra quatro orientações, definidas pelo ângulo θ , de um momento de dipolo magnético μ → em um campo magnético B → .

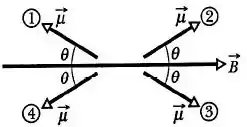
Ordene, começando pelo maior, o trabalho realizado por um agente externo sobre o dipolo para as três rotações seguintes: 2 → 1 , 2 → 4 e 2 → 3 .

a 2 → 1 , 2 → 4 e 2 → 3 ;

b 2 → 3 , 2 → 1 , 2 → 4 ;

c 2 → 1 e 2 → 3 empatados, 2 → 4 ;

d 2 → 1 e 2 → 4 empatados, 2 → 3 ;

e 2 → 4 , 2 → 3 , 2 → 1 ;

Passo 1

Por definição, o trabalho realizado por um agente externo sobre o dipolo pode ser escrito como:

W e x t = Δ U = U f - U i

Onde U é a energia potencial magnética que, no caso do dipolo, é dada por:

U = - μ → ∙ B → = - μ B cos ⁡ θ

Agora vamos analisar cada rotação.

Passo 2

Rotação 2 → 1 :

W 2 → 1 = U 1 - U 2

W 2 → 1 = - μ B cos ⁡ θ 1 + μ B cos ⁡ θ 2

Onde cos ⁡ θ 1 = - cos ⁡ θ e cos ⁡ θ 2 = cos ⁡ θ , logo:

W 2 → 1 = - μ B - cos ⁡ θ + μ B cos ⁡ θ

W 2 → 1 = 2 μ B cos ⁡ θ

Passo 3

Rotação 2 → 4 :

W 2 → 4 = U 4 - U 2

W 2 → 4 = - μ B cos ⁡ θ 4 + μ B cos ⁡ θ 2

Onde cos ⁡ θ 4 = - cos ⁡ θ e cos ⁡ θ 2 = cos ⁡ θ , logo:

W 2 → 4 = - μ B - cos ⁡ θ + μ B cos ⁡ θ

W 2 → 4 = 2 μ B cos ⁡ θ

Passo 4

Rotação 2 → 3 :

W 2 → 3 = U 2 - U 3

W 2 → 3 = - μ B cos ⁡ θ 2 + μ B cos ⁡ θ 3

Onde cos ⁡ θ 2 = cos ⁡ θ e cos ⁡ θ 3 = cos ⁡ θ , logo:

W 2 → 3 = - μ B cos ⁡ θ + μ B cos ⁡ θ

W 2 → 3 = 0

Assim, finalmente:

W 2 → 1 = W 2 → 4 > W 2 → 3

Resposta

d 2 → 1 e 2 → 4 empatados, 2 → 3 ;

Exercícios de Livros Relacionados

Uma esfera uniforme, sólida, uniformemente carregada, de raio R , tem uma densidade volumétrica de carga ρ . A esfera gira em torno de um eixo que passa pelo seu centro com rapidez angular ω . Determi
Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo 2,30 A · m 2 . (b) Determine o valor máximo do torque a que a bo
Uma espira circular com 8,0 cm de raio é percorrida por uma corrente de 0,20 A . Um vetor de comprimento unitário, paralelo ao momento dipolar μ → da espira, é dado por 0,60 i ^ – 0,80 j ^ . (Esse vet
Na Fig. 28-50a, duas espiras concêntricas, situadas no mesmo plano, são percorridas por correntes em sentidos contrários. A corrente i 1 na bobina 1 é fixa e a corrente i 2 na bobina 2 é variável. A F
A bobina da Fig. 28-49 conduz uma corrente i = 2,00 A no sentido indicado, é paralela ao plano x z , possui 3,00 espiras, tem uma área de 4,00 × 10 - 3 m 2 e está submetida a um campo magnético unifor