Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.
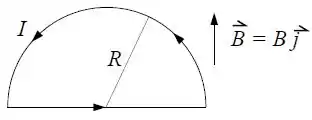
Determine a força magnética total (vetor) sobre a parte retilínea do condutor.
Determine a força magnética total (vetor) sobre a parte curva do condutor.
Determine o vetor torque exercido por sobre o circuito.
Passo 1
Determine a força magnética total (vetor) sobre a parte retilínea do condutor.
Por definição, a força magnética sobre uma espira é dada por:
Onde está sempre na mesma direção e sentido da corrente.
No caso de um condutor retilíneo, podemos dar uma simplificada nesse cara que, agora, terá essa cara:
Onde, novamente, tem a direção e sentido da corrente.
Passo 2
Nesse problema, olhando a figura, podemos concluir que:
Portanto:
Passo 3
Determine a força magnética total (vetor) sobre a parte curva do condutor.
Aqui, como se trata se um condutor curvado, vamos usar essa expressão para a força magnética:
Beleza, vamos dar uma olhada no vetor nesse caso:
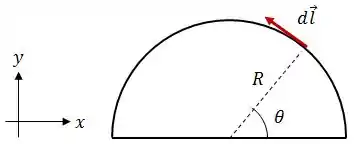
Daqui podemos decompor o vetor em componentes nas direções e .
Substituindo isso na expressão de , teremos:
Agora é só organizar esse cara e fazer as contas:
Passo 4
Determine o vetor torque exercido por sobre o circuito.
Por definição, o torque sobre uma espira é dada por:
Onde é o momento dipolar elétrico, definidor por:
Onde é o vetor cujo módulo é igual à área que do circuito, direção perpendicular ao plano do circuito e sentido dado pela regra da mão direita.
Como a corrente flui no sentido anti-horário, pela regra da mão direita, teremos:
Logo:
E, finalmente, o torque será dado por:
Resposta