Demonstre que geometricamente o produto misto é igual em módulo ao volume do paralelepípedo determinado pelos vetores e .

A figura a seguir vai nos ajudar bastante!!

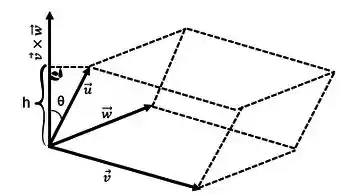
Sabemos das nossas aulas de geometria do ensino médio que o volume de uma paralelepípedo é:

Na figura acima nossa base é formada pelos vetores , então a área da nossa base como vimos em produto vetorialé igual a:

E quanto vale a altura? Bem, a altura é:

Deve ser o módulo do cosseno, pois não existe comprimento negativo, e o cosseno pode ser negativo.

Então, o volume do paralelepípedo fica:

Bem, e o que isso prova? Ainda nada hehe, porque temos que provar agora que módulo do produto misto vale isso ;).

Se dissermos que

Pelo produto misto teremos:

Pela propriedade do produto escalar temos:

Quem é o módulo de ?

Então,

Portanto, partindo do volume generalizado e partindo do módulo do produto misto conseguimos mostrar que realmente o módulo do produto misto corresponde aovolume do paralelepípedo.