Para que valor de os pontos são coplanares?
Passo 1
Poxa vida!!! Mas, esse problema é o mesmo do anterior!!

Ele pode ser parecido, mas não é igual não. Sabe pq? Porque no anterior o problema nos dava os vetores bonitinhos e aqui não, é nos dado os pontos. Então, tome cuidado, produto misto é entre VETORES, e não entre pontos.
Passo 2
Bora montar os vetores!!!
Como vimos num problema anterior se três vetores são coplanares, então o volume do paralelepípedo que seria formado por eles é ZERO. E por costume escolheremos os vetores partindo de uma mesma origem. Vou escolher o ponto . Então, teremos os vetores:
Passo 3
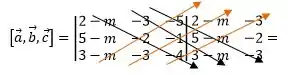
Agora sim, é resolver o produto misto entre os vetores para que os vetores sejam coplanares, ou seja, produto misto igual a ZEROOO.