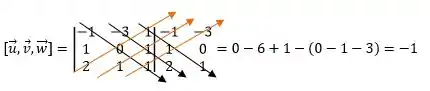
Calcule sendo .
Passo 1
Essa notação ela não é tão convencional, mas também é utilizada para indicar um produto misto. Então, temos que:
Sendo que nos foram fornecidos os três vetores comas suas coordenadas
Passo 2
Como vimos na teoria calcular o produto misto é na verdade calcular um determinante de uma matriz sendo que cada linha da matriz representa um dos vetores, e cada coluna uma das componentes, como a seguir:
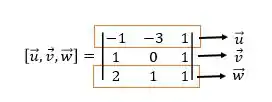
Passo 3
Agora é calcular o determinante.
Resposta
Exercícios de Livros Relacionados
74. Dados os pontos A 1 , - 2,3 ,B 2 , - 1 , - 4 , C 0,2 , 0 e D - 1 , m , 1 , determinar o valor de m para que seja de 20 unidade de volume o volume do paralelepípedo determinado pelos vetores A B ,
Use o produto misto para determinar se os pontos P 1,0 , 1 , Q 2,4 , 6 , R 3 , - 1,2 e S 6,2 , 8 pertencem ao mesmo plano.
Calcular o volume de tetraedro de base A B C e vértice P , sendo A 2,0 , 0 ,B 2,4 , 0 ,C 0,3 , 0 eP ( 2 , - 2,9 ) . Qual a altura relativa ao vértice P ?
Representar graficamente o tetraedro ABCD e calcular seu volume, sendo A 1,1 , 0 ,B 6,4 , 1 ,C 2,5 , 0e D ( 0,3 , 3 ) .
Calcular a distância do ponto D ( 2,5 , 2 ) ao plano determinado pelos pontos A 3,0 , 0 ,B 0 , - 3,0eC ( 0,0 , 3 ) .