Considere os pontos
e os vetores:
(a) Determine se existe um plano que contém os pontos A, B, C e D.
Passo 1
(a) Vamos começar definindo os vetores:
Se existir um único plano que contém os pontos A, B, C e D, então os vetores e serão coplanares.
Isso significa que o produto misto entre esses 3 caras será 0.
Vamos ver se isso vai ser verdade calculando o produto misto:
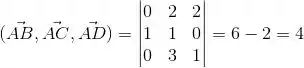
E claramente .
Então esses 3 vetores não são coplanares e não existe um único plano que contém os pontos A, B, C e D.
Resposta
(a) Não existe um único plano que contém os pontos A, B, C e D.